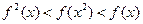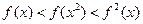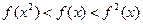题目内容
已知函数 .
.
(1)求f(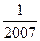 )+f(-
)+f(-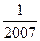 )的值;
)的值;
(2)当x∈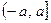 (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时,
f(x)是否存在最小值, 若存在, 求出最小值; 若不存在, 请说明理由.
 .
.(1)求f(
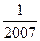 )+f(-
)+f(-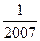 )的值;
)的值; (2)当x∈
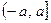 (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时, f(x)是否存在最小值, 若存在, 求出最小值; 若不存在, 请说明理由.
(1)0,(2)当x∈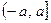 (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时,
f(x)存在最小值,,且最小值为f(a)= -a+log2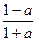
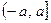 (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时, f(x)存在最小值,,且最小值为f(a)= -a+log2
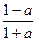
(1)f(x)的定义域是(-1, 1),
∵f(-x)=-(-x)+log2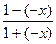 =-(-x+log2
=-(-x+log2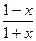 )="-" f(x)
)="-" f(x)
∴f(x)为奇函数. ∴f(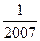 )+f(-
)+f(-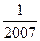 )="0. " ……5分
)="0. " ……5分
(直接运算也可以)
(2)设-1< x1< x2 <1,
∵f(x2)-f(x1)=" -" x2+ log2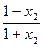 -[- x1+ log2
-[- x1+ log2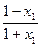 ] ……7分
] ……7分
="(" x1- x2)+ log2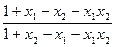 ,
,
∵x1- x2< 0, 1+x1-x2- x1x2-(1+x2-x1- x1x2)=2(x1- x2)<0,
∴1+x1-x2- x1x2< 1+x2-x1- x1x2.
∴0<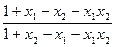 <1.
<1.
∴log2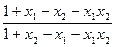 < 0.
< 0.
∴f(x2)-f(x1) < 0. ∴f(x)在(-1, 1)上单调递减. ……10分
∴当x∈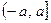 (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时,
f(x)存在最小值,,且最小值为f(a)= -a+log2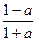 ……12分
……12分
∵f(-x)=-(-x)+log2
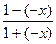 =-(-x+log2
=-(-x+log2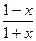 )="-" f(x)
)="-" f(x)∴f(x)为奇函数. ∴f(
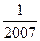 )+f(-
)+f(-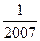 )="0. " ……5分
)="0. " ……5分(直接运算也可以)
(2)设-1< x1< x2 <1,
∵f(x2)-f(x1)=" -" x2+ log2
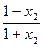 -[- x1+ log2
-[- x1+ log2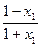 ] ……7分
] ……7分="(" x1- x2)+ log2
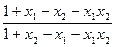 ,
, ∵x1- x2< 0, 1+x1-x2- x1x2-(1+x2-x1- x1x2)=2(x1- x2)<0,
∴1+x1-x2- x1x2< 1+x2-x1- x1x2.
∴0<
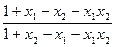 <1.
<1.∴log2
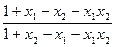 < 0.
< 0. ∴f(x2)-f(x1) < 0. ∴f(x)在(-1, 1)上单调递减. ……10分
∴当x∈
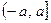 (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时, f(x)存在最小值,,且最小值为f(a)= -a+log2
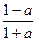 ……12分
……12分
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
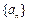 的前n项和
的前n项和 满足:
满足: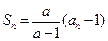 (a为常数,且
(a为常数,且 ). (Ⅰ)求
). (Ⅰ)求 ,若数列
,若数列 为等比数列,求a的值;
为等比数列,求a的值;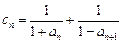 ,数列
,数列 的前n项和为Tn .
的前n项和为Tn . .
. ,单位是m/s,其中
,单位是m/s,其中 表示鱼的耗氧量的单位数.
表示鱼的耗氧量的单位数. 、
、 两地同时开出.已知
两地同时开出.已知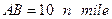 ,甲乙两船的速度分别是16 n mile/h和12 n mile/h,求多少时间后,两船距离最近,最近距离是多少?
,甲乙两船的速度分别是16 n mile/h和12 n mile/h,求多少时间后,两船距离最近,最近距离是多少?



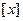 表示不超过
表示不超过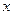 的最大整数,如
的最大整数,如 ,
,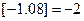 ,定义函数
,定义函数 .给出下列四个命题:①函数
.给出下列四个命题:①函数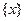 的定义域是R,值域为
的定义域是R,值域为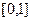 ;②方程
;②方程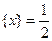 有无数个解;③函数
有无数个解;③函数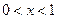 时,
时,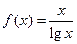 ,则下列大小关系正确的是( )
,则下列大小关系正确的是( )