题目内容
 设函数f(x)=
设函数f(x)=| ax+b |
| x2+c |
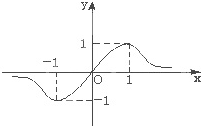
分析:由函数图象可得f(0)=
=0,解得b=0,又f(1)=
=1,故a=c+1,再由f′(1)=0,可得c的值,进而可得a的值,故可比较大小.
| b |
| c |
| a |
| 1+c |
解答:解:由函数图象可得f(0)=
=0,解得b=0,
又f(1)=
=1,故a=c+1,
又f′(x)=
=
,
由图可知x=1为函数的极值点,故f′(1)=0,
即-a+ac=0,解得c=1,a=2,
故a>c>b,
故选B
| b |
| c |
又f(1)=
| a |
| 1+c |
又f′(x)=
| a(x2+c)-(ax+b) |
| (x2+c)2 |
| -ax2-2bx+ac |
| (x2+c)2 |
由图可知x=1为函数的极值点,故f′(1)=0,
即-a+ac=0,解得c=1,a=2,
故a>c>b,
故选B
点评:本题考查由函数的图象求解函数的系数的问题,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |