题目内容
(2011•开封一模)函数y=x和y=x3的图象所围成的图形的面积为
.
| 1 |
| 2 |
| 1 |
| 2 |
分析:联立
,求其交点坐标,再利用定积分求出即可.
|
解答: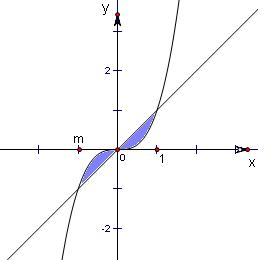 解:联立
解:联立
,解得
,或
或
,
即函数y=x3与函数y=x的图象的交点(0,0),(1,1),(-1,-1).
于是所求的面积=2
(x-x3)dx=2(
-
)
=
.
故答案为
.
 解:联立
解:联立
|
|
|
|
即函数y=x3与函数y=x的图象的交点(0,0),(1,1),(-1,-1).
于是所求的面积=2
| ∫ | 1 0 |
| x2 |
| 2 |
| x4 |
| 4 |
| | | 1 0 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:利用定积分求封闭图形的面积是求面积的通法,应熟练掌握.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 (2011•开封一模)某校为了解高三学生在寒假期间的学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图),则这100名同学中学习时间在6到8小时内的人数为( )
(2011•开封一模)某校为了解高三学生在寒假期间的学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图),则这100名同学中学习时间在6到8小时内的人数为( )