题目内容
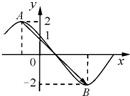如图所示为函数f（x）=2cos（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中 
，那么ω和φ的值分别为
- A.
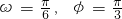
- B.
- C.
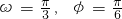
- D.
B
分析：先确定函数的周期，由图可知，AB间的纵向距离为4，故可由勾股定理计算AB间的横向距离，即半个周期，进而得ω值，再利用函数图象过点（0，1），且此点在减区间上，代入函数解析式即可计算φ值
解答：由图可知函数的振幅为2，半周期为AB间的横向距离，
=
=3，
∴T=6，即
=6
∴ω=
由图象知函数过点（0，1）
∴1=2cosφ
∴φ=2kπ+，k∈Z
∵0≤φ≤π
∴φ=，
故选B
点评：本题考查了三角函数的图象和性质，由y=Asin（ωx+φ）的部分图象确定其解析式的方法，三角函数周期，初相的意义
分析：先确定函数的周期，由图可知
，AB间的纵向距离为4，故可由勾股定理计算AB间的横向距离，即半个周期，进而得ω值，再利用函数图象过点（0，1），且此点在减区间上，代入函数解析式即可计算φ值解答：由图可知函数的振幅为2，半周期为AB间的横向距离，
==3，∴T=6，即
=6∴ω=
由图象知函数过点（0，1）
∴1=2cosφ
∴φ=2kπ+
，k∈Z∵0≤φ≤π
∴φ=
，故选B
点评：本题考查了三角函数的图象和性质，由y=Asin（ωx+φ）的部分图象确定其解析式的方法，三角函数周期，初相的意义
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，
（2012•佛山二模）如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）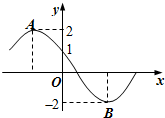
如图所示为函数f（x）=Asin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）
如图所示为函数f（x）=2cos（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中
（2012•广安二模）如图所示为函数f（x）=x3+bx2+cx+d的导函数f′（x）的图象，则函数