题目内容
 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,| π | 2 |
-1
-1
.分析:由图象可得A=2,2sinφ=1,再由0≤φ≤π,结合图象可得φ 的值.再由A,B两点之间的距离为5,求出周期,可得ω的值,从而求得函数f(x)的解析式,f(1)的值可求.
解答:解:由图象可得A=2,2sinφ=1,即 sinφ=
.再由
<φ<π,结合图象可得φ=
.
再由A,B两点之间的距离为5,可得25=16+(
)2,解得ω=
.
故函数f(x)=2sin(
x+
),
故f(1)=2sin
=-1,
故答案为:-1.
| 1 |
| 2 |
| π |
| 2 |
| 5π |
| 6 |
再由A,B两点之间的距离为5,可得25=16+(
| π |
| ω |
| π |
| 3 |
故函数f(x)=2sin(
| π |
| 3 |
| 5π |
| 6 |
故f(1)=2sin
| 7π |
| 6 |
故答案为:-1.
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•佛山二模)如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
(2012•佛山二模)如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )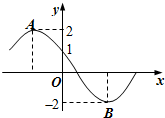 如图所示为函数f(x)=Asin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
如图所示为函数f(x)=Asin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( ) 如图所示为函数f(x)=2cos(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中
如图所示为函数f(x)=2cos(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中 (2012•广安二模)如图所示为函数f(x)=x3+bx2+cx+d的导函数f′(x)的图象,则函数
(2012•广安二模)如图所示为函数f(x)=x3+bx2+cx+d的导函数f′(x)的图象,则函数