题目内容
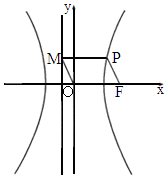
(22)如图,双曲线M为左准线与渐近线在第二象限内的交点,且![]() .
.
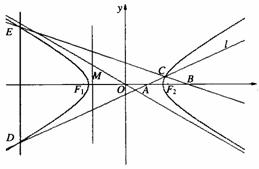
(Ⅰ)求双曲线的方程;
(Ⅱ)设A(m,0)和B(![]() ,0)(0<m<1)是x轴上的两点.过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.
,0)(0<m<1)是x轴上的两点.过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.
本小题主要考查双曲线的标准方程和几何性质、直线方程、平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法,考查推理和运算能力.
(Ⅰ)解:根据题设条件,F1(-c,0),F2(c,0).设点M(x,y).则x、y满足
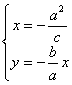

因e=![]() ,解得M(-
,解得M(-![]() ),故
),故
![]()
=![]()
利用a2+b2=c2,得c2=![]() ,于是a2=1,b2=
,于是a2=1,b2=![]() .因此,所求双曲线方程为
.因此,所求双曲线方程为
x2-4y2=1.
(Ⅱ)解:设点C(x1,y1),D(x2,y2),E(x3,y3),则直线l的方程为
y=![]() (x-m).
(x-m).
于是C(x1,y1)、D(x2,y2)两点坐标满足
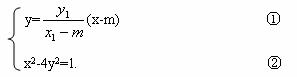
将①代入②得
(x12-2x1m+m2-4y12)x2+8my12x-4y12m2-x12+2mx1-m2=0.
由x21-4y21=1 (点C在双曲线上),上面方程可化简为
(m2-2x1m+1)x2+8my12x-(x12-2mx1+m2x12)=0.
由已知,显然m2-2x1m+1≠0.于是x1x2=-![]() .因为x1≠0,得
.因为x1≠0,得
x2=![]()
同理,C(x1,y1)、E(x3,y3)两点坐标满足
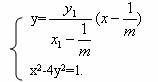
可解得
x3=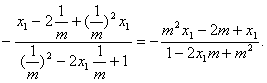
所以x2=x3,故直线DE垂直于x轴.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,已知椭圆
如图,已知椭圆 (2012•湖北)如图,双曲线
(2012•湖北)如图,双曲线 如图,在中
如图,在中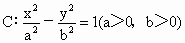 的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点.已知四边形OFPM为平行四边形,
的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点.已知四边形OFPM为平行四边形,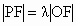 .
.