题目内容
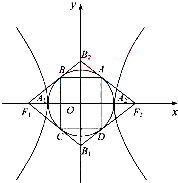 (2012•湖北)如图,双曲线
(2012•湖北)如图,双曲线| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)双曲线的离心率e=
| ||
| 2 |
| ||
| 2 |
(Ⅱ)菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值
| S1 |
| S2 |
| ||
| 2 |
| ||
| 2 |
分析:(Ⅰ)直线B2F1的方程为bx-cy+bc=0,所以O到直线的距离为
,根据以A1A2为直径的圆内切于菱形F1B1F2B2,可得
=a,由此可求双曲线的离心率;
(Ⅱ)菱形F1B1F2B2的面积S1=2bc,求出矩形ABCD的长与宽,从而求出面积S2=4mn=
,由此可得结论.
| |bc| | ||
|
| |bc| | ||
|
(Ⅱ)菱形F1B1F2B2的面积S1=2bc,求出矩形ABCD的长与宽,从而求出面积S2=4mn=
| 4a2bc |
| b2+c2 |
解答:解:(Ⅰ)直线B2F1的方程为bx-cy+bc=0,所以O到直线的距离为
∵以A1A2为直径的圆内切于菱形F1B1F2B2,
∴
=a
∴(c2-a2)c2=(2c2-a2)a2
∴c4-3a2c2+a4=0
∴e4-3e2+1=0
∵e>1
∴e=
(Ⅱ)菱形F1B1F2B2的面积S1=2bc
设矩形ABCD,BC=2m,BA=2n,∴
=
∵m2+n2=a2,∴m=
,n=
∴面积S2=4mn=
∴
=
=
∵bc=a2=c2-b2
∴b=
c
∴
=
故答案为:
,
| |bc| | ||
|
∵以A1A2为直径的圆内切于菱形F1B1F2B2,
∴
| |bc| | ||
|
∴(c2-a2)c2=(2c2-a2)a2
∴c4-3a2c2+a4=0
∴e4-3e2+1=0
∵e>1
∴e=
| ||
| 2 |
(Ⅱ)菱形F1B1F2B2的面积S1=2bc
设矩形ABCD,BC=2m,BA=2n,∴
| m |
| n |
| c |
| b |
∵m2+n2=a2,∴m=
| ac | ||
|
| ab | ||
|
∴面积S2=4mn=
| 4a2bc |
| b2+c2 |
∴
| S1 |
| S2 |
| b2+c2 |
| 2a2 |
| b2+c2 |
| 2bc |
∵bc=a2=c2-b2
∴b=
-1+
| ||
| 2 |
∴
| S1 |
| S2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
| ||
| 2 |
点评:本题考查圆与圆锥曲线的综合,考查双曲线的性质,面积的计算,解题的关键是确定几何量之间的关系.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 (2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ=
(2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ= (2012•湖北)如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
(2012•湖北)如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是( ) (2012•湖北)如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
(2012•湖北)如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )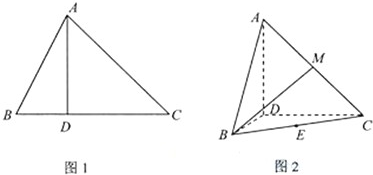 (2012•湖北)如图1,∠ACB=45°,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90°(如图2所示),
(2012•湖北)如图1,∠ACB=45°,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90°(如图2所示),