题目内容
如图，在中tan| C |
| 2 |
| 1 |
| 2 |
| AH |
| AB |
| AC |
2
2
．分析：如图，利用图中焦点三角形AHC，结合双曲线的离心率的定义，充分利用直角三角形的几何性质，即可求得双曲线的离心率．
解答：解：∵
•
=0，
所以AH⊥BC，
∴tanC=
=
=
，
令AH=4t，AC=5t，
所以e=
=
=2．
故答案为：2．
| AH |
| CB |
所以AH⊥BC，
∴tanC=
2tan
| ||
1-tan2
|
| 1 | ||
1-
|
| 4 |
| 3 |
令AH=4t，AC=5t，
所以e=
| AH |
| CA-CH |
| 4t |
| 5t-3t |
故答案为：2．
点评：本题考查结合双曲线的离心率的定义，圆锥曲线中的离心率反映了圆锥曲线的形状，也反映了圆锥曲线上的点到焦点和到准线的距离的关系，充分利用直角三角形的几何性质，即可求得双曲线的离心率．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图，在△ABC中，tan
=
，
•
=0，则过点C，以A、H为两焦点的双曲线的离心率为（ ）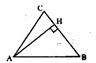
| C |
| 2 |
| 1 |
| 2 |
| AH |
| BC |
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|