题目内容
(本题满分12分)
如图,四边形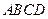 是
是 边长为2的正方形,
边长为2的正方形,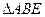 为等腰三角形
为等腰三角形 ,
,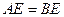 ,平面
,平面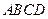 ⊥平面
⊥平面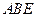 ,点
,点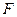 在
在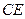
 上,且
上,且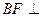 平面
平面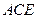 .
.

(Ⅰ)判断直线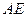 与平面
与平面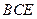 是否垂直,并说明理由;
是否垂直,并说明理由;
(Ⅱ)求点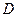 到平面
到平面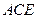
 的距离.
的距离.
如图,四边形
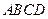 是
是 边长为2的正方形,
边长为2的正方形,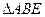 为等腰三角形
为等腰三角形 ,
,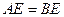 ,平面
,平面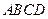 ⊥平面
⊥平面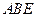 ,点
,点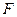 在
在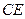
 上,且
上,且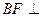 平面
平面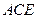 .
.
(Ⅰ)判断直线
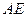 与平面
与平面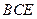 是否垂直,并说明理由;
是否垂直,并说明理由;(Ⅱ)求点
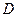 到平面
到平面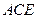
 的距离.
的距离.、证明:(Ⅰ)因为BF⊥平面ACE,所以BF⊥AE.
因为平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以BC⊥平面ABE,从而BC⊥AE.

于是AE⊥平面BCE. ……6分
(Ⅱ)方法一:连结BD交AC与点M,则点M是BD的中点,
所以点D与点B到平面ACE的距离相等.
因为BF⊥平面ACE,所以BF为点B到平面ACE的距离.
因为AE⊥平面BCE,所以AE⊥BE.
又AE=BE,所以△AEB是等腰直
 角三角形.
角三角形.因为AB=2,所以BE=
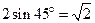 .
. 在Rt△CB
 E中,
E中,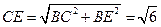 .
. 所以
 .
.故点D到平面ACE的距离是
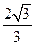 . ……12分
. ……12分 方法二:过点E作EG⊥AB,垂足为G,因为平面ABCD⊥平面ABE,所以EG⊥平面ABCD.
因为AE⊥平面BCE,所以AE⊥BE.又AE=BE,所以△AEB是等腰直角三角形,从而G为AB的中点.又AB=2,所以EG=1.
因为AE⊥平面BCE ,所以AE⊥EC.
又AE=BE=
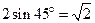 ,
,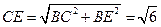 .
. 设点D到平面ACE的距离为h,因为VD-ACE=VE-ACD,则
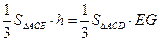 .
.所以
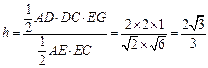 ,故点D到平面ACE的距离是
,故点D到平面ACE的距离是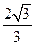 . 12分
. 12分略

练习册系列答案
相关题目
 底面ABCD,PD=DC,
底面ABCD,PD=DC, 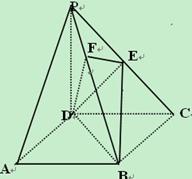

 于同一平面的两平面互相平行;
于同一平面的两平面互相平行;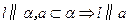
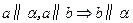
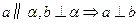
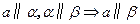
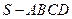 中,底面
中,底面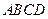 为矩形,平面
为矩形,平面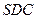
 底面
底面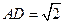 ,
,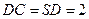 ,
,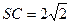 ,点
,点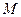 是侧棱
是侧棱 的中点.
的中点.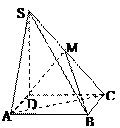
 平面
平面 的大小.
的大小.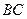 求一点
求一点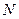 ,使点
,使点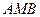 的距离为
的距离为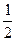 .
.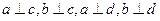 ,那么
,那么 面ABCD,
面ABCD,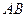 ∥
∥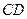 ,AD=CD=1,∠
,AD=CD=1,∠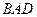 =120°,
=120°,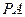 =
=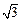 ,∠
,∠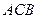 =90°,M是线段PD上的一点(不包括端点).
=90°,M是线段PD上的一点(不包括端点).