题目内容
解答题
已知函数f(x)=x2-1(x≥1)的曲线为C1,曲线C2与C1关于直线y=x对称.
(1)求曲线C2的方程y=g(x);
(2)设函数y=g(x)的定义域为M,x1,x2∈M,且x1≠x2,求证:|g(x1)-g(x2)|<|x1-x2|:
(3)设A、B为曲线C2上任意不同两点,证明直线AB与直线y=x必相交.
答案:
解析:
解析:
|
(1)曲线C1和C2关于直线y=x对称,则y(x)为f(x)的反函数. 由y=x2-1(x≥1)得x= ∴曲线C2的方程g(x)= (2)设x1>x2∈M,且x1≠x2. 则x1-x2≠0且x1≥0,x2≥0. ∴|g(x1)-g(x2)|=| (3)证明:设A、B为曲线C2上任意不同两点(x1,y1),(x2,y2). x1,x2∈M,且x1≠x2,由(2)知 |kAB|= ∴直线AB的斜率|kAB|≠±1. 而直线y=x的斜率为1. ∴直线AB与直线y=x必相交. |

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
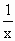 +2的图像关于点A(0,1)对称.
+2的图像关于点A(0,1)对称.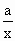 ,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.