题目内容
解答题
已知函数f(x)=x3-x+c定义在区间[0,1]上,x1、x2∈[0,1]且x1≠x2.
求证:(1)f(0)=f(1);
(2)|f(x2)-f(x1)|<2|x2-x1|;
(3)|f(x2)-f(x1)|<1.
答案:
解析:
解析:
|
证明:(1)∵f(x)=x3-x+c,∴f(0)=c, ∴f(1)=c,∴f(0)=f(1). (2)|f(x2)-f(x1)|=|(x23-x2+c)-(x13-x1+c)| =|(x23-x13)-(x2-x1)| =|x2-x1|·|x22+x12+x1x2-1|. ∵x1,x2∈[0,1]且x1≠x2, ∴x22+x12+x1x2∈(0,3). ∴|x22+x12+x1x2-1|<2, ∴|f(x2)-f(x1)|<2|x2-x1|. (3)∵f(0)=f(1), ∴|f(x2)-f(x1)|=|f(x2)-f(1)+f(0)-f(x1)|≤|f(x2)-f(1)|+|f(0)-f(x1)|<2|x2-1|+2|0-x1|. 又∵x1,x2∈[0,1] ∴|f(x2)-f(x1)|<2(1-x2)+2x1=2-2x2+2x1 ① 当x2>x1时,|f(x2)-f(x1)|<2|x2-x1|=2x2-2x1 ② ①+②得|f(x2)-f(x1)|<1. 同理可证,当x2<x1时,也有|f(x2)-f(x1)|<1. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
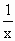 +2的图像关于点A(0,1)对称.
+2的图像关于点A(0,1)对称.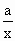 ,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.