题目内容
（08年重点中学模拟理） （12分）如图，在四棱锥P―ABCD中，PA⊥平面ABCD，四边形ABCD为直角梯形，AD//BC且AD>BC，∠DAB=∠ABC=90°，PA=
，AB=BC=1。M为PC的中点。
（1）求二面角M―AD―C的大小；
（2）如果∠AMD=90°，求线段AD的长。
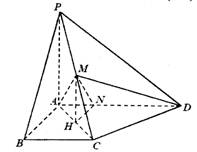
解析：（1）取AC的中点H，连MH，则MH//PA，所以MH⊥平面ABCD，过H作HN⊥AD于N，连MN，由三垂线定理可得MN⊥AD，
则∠MNH就为所求的二面角的平面角。………………2分
AH
在Rt△ANH中，
则在Rt△MHN中，
故所示二面角的大小为
………………6分
（2）若AM⊥MD，又因为PA=AC=
，M为PC的中点，
则AM⊥PC，所以AM⊥平面PCD，则AM⊥CD。………………8分
AM在平面ABCD的射影为CD，由三垂线定理可知其等价于AC⊥CD，…………10分
此时△ACD为等腰直角三角形，所以AD=AC=2。………………12分
练习册系列答案
津桥教育计算小状元系列答案
相关题目
图像上相邻的两个对称轴的距离是
的值；
上的最大值和最小值。
为与桌面接触的4个面上数字中偶数的个数，求
处取得极值。
处取得极大值
时取得最小值，求c的取值范围。
外一点，设k1,k2分别是过点P的圆C两条切线的斜率。
，求点P的轨迹M的方程，并指出曲线M所在圆锥曲线的类型。