题目内容
(2012•福建)选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l上两点M,N的极坐标分别为(2,0),(
,
),圆C的参数方程
(θ为参数).
(Ⅰ)设P为线段MN的中点,求直线OP的平面直角坐标方程;
(Ⅱ)判断直线l与圆C的位置关系.
在平面直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l上两点M,N的极坐标分别为(2,0),(
2
| ||
| 3 |
| π |
| 2 |
|
(Ⅰ)设P为线段MN的中点,求直线OP的平面直角坐标方程;
(Ⅱ)判断直线l与圆C的位置关系.
分析:(Ⅰ)设P为线段MN的中点,求直线OP的平面直角坐标方程;
(Ⅱ)求出圆的圆心与半径,判断圆心与直线的距离与半径的关系,即可判断直线l与圆C的位置关系.
(Ⅱ)求出圆的圆心与半径,判断圆心与直线的距离与半径的关系,即可判断直线l与圆C的位置关系.
解答:解:(Ⅰ)M,N的极坐标分别为(2,0),(
,
),
所以M、N的直角坐标分别为:M(2,0),N(0,
),P为线段MN的中点(1,
),
直线OP的平面直角坐标方程y=
x;
(Ⅱ)圆C的参数方程
(θ为参数).它的直角坐标方程为:(x-2)2+(y+
)2=4,
圆的圆心坐标为(2,-
),半径为2,
直线l上两点M,N的极坐标分别为(2,0),(
,
),
方程为y=
(x-2),即3πx+(12-4
)y-6π=0.
圆心到直线的距离为:
=
<
<2,
所以,直线l与圆C相交.
2
| ||
| 3 |
| π |
| 2 |
所以M、N的直角坐标分别为:M(2,0),N(0,
2
| ||
| 3 |
| ||
| 3 |
直线OP的平面直角坐标方程y=
| ||
| 3 |
(Ⅱ)圆C的参数方程
|
| 3 |
圆的圆心坐标为(2,-
| 3 |
直线l上两点M,N的极坐标分别为(2,0),(
2
| ||
| 3 |
| π |
| 2 |
方程为y=
| 3π | ||
4
|
| 3 |
圆心到直线的距离为:
|6π-
| ||||
|
12(
| ||
|
12(
| ||
| 3π |
所以,直线l与圆C相交.
点评:本题考查圆的参数方程,极坐标方程与直角坐标方程的转化,直线与圆的位置关系,考查计算能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
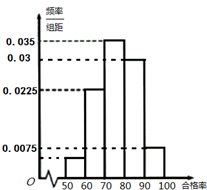 (2012•福建模拟)21、某工厂共有工人40人,在一次产品大检查中每人的产品合格率(百分比)绘制成频率分布直方图,如图所示.
(2012•福建模拟)21、某工厂共有工人40人,在一次产品大检查中每人的产品合格率(百分比)绘制成频率分布直方图,如图所示.