题目内容
圆 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )
A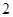 B
B  C
C  D
D 
 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )A
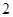 B
B  C
C  D
D 
B
专题:计算题.
分析:先将圆x2+y2-2x-2y+1=0转化为标准方程:(x-1)2+(y-1)2=1,明确圆心和半径,再求得圆心(1,1)到直线x-y=2的距离,最大值则在此基础上加上半径长即可.
解答:解:圆x2+y2-2x-2y+1=0可化为标准形式:(x-1)2+(y-1)2=1,
∴圆心为(1,1),半径为1
圆心(1,1)到直线x-y=2的距离d=
 ,
,则所求距离最大为1+
 ,
,故选B.
点评:本题主要考查直线与圆的位置关系,当考查圆上的点到直线的距离问题,基本思路是:先求出圆心到直线的距离,最大值时,再加上半径,最小值时,再减去半径.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 :
: 与
与 轴交于点
轴交于点 、
、
 ,与
,与 轴交于点
轴交于点 ,其中
,其中
 交于不同两点E
交于不同两点E ,F,问是否存在直线l,使得向量
,F,问是否存在直线l,使得向量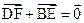 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.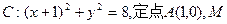 为圆上一动点,点
为圆上一动点,点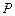 在
在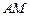 上,点
上,点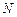 在
在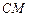 上,且满足
上,且满足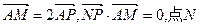 的轨迹为曲线
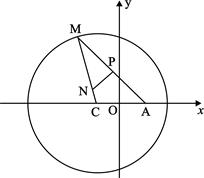
的轨迹为曲线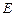 .
.
 两点
两点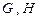 (点
(点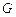 在点
在点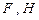 之间),且满足
之间),且满足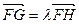 ,求
,求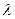 的取值范围.
的取值范围. 如果直线
如果直线 与圆
与圆 交于M、N两点,且M、N关于直线2x+y=0对称,则直线l被圆截得的弦长为_________
交于M、N两点,且M、N关于直线2x+y=0对称,则直线l被圆截得的弦长为_________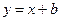 与曲线
与曲线 有且仅有一个公共点,则b的取值范围是 .
有且仅有一个公共点,则b的取值范围是 .  的直线
的直线 与曲线
与曲线 有公共点,则直线
有公共点,则直线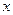 轴的正半轴上,且与直线
轴的正半轴上,且与直线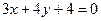 相切,则此圆的方程是 ( )
相切,则此圆的方程是 ( )


