题目内容
如图,已知两个正方形ABCD 和DCEF不在同一平面内,且平面ABCD ⊥平面DCEF,M,N分别为AB,DF的中点。

(1)求直线MN与平面ABCD所成角的正弦值;
(2)求异面直线ME与BN所成角的余弦值。

(1)求直线MN与平面ABCD所成角的正弦值;
(2)求异面直线ME与BN所成角的余弦值。
(1) (2)
(2)
 (2)
(2)
试题分析:(1)如图,连接MD

∵平面ABCD ⊥平面DCEF ①
ND⊥CD,ND
 平面DCEF ②
平面DCEF ②CD=面ABCD
 面DCEF ③
面DCEF ③由①②③知ND⊥平面ABCD,
∴∠DMN即为MN 与面ABCD所成角,
设CD=a,则ND=
 ,MN=
,MN= ,
,∴
 .
.(2)如图,在CD的延长线上取点G,使DG=DC,再以DG为公共边作正方形DGUA及DGVF,

H,K分别为GV,NH之中点,连接MK,EK.
∵NK∥CD,NK=
 CD,BM∥CD,BM=
CD,BM∥CD,BM= CD,
CD,∴四边形BMKN为平行四边形,∴BN∥MK,
∴∠EMK即为异面直线BN与ME所成角,
设CD=a,则 ME=BN=
 ,EK=
,EK= ,
,由余弦定理得
 .
.点评:点评:立体几何问题,主要是考查学生的空间想象能力和逻辑推理能力,解决此类问题时,要紧扣相应的判定定理和性质定理,要将定理中要求的条件一一列举出来,缺一不可.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
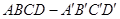 棱长为1,
棱长为1,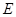 是
是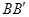 的中点,
的中点,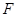 是
是 的中点.
的中点. 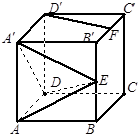
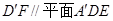 ;
;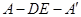 的余弦值.
的余弦值.
 的距离.
的距离. 

 ,动点P.Q分别在面α.β内,P到β的距离为
,动点P.Q分别在面α.β内,P到β的距离为 ,Q到α的距离为
,Q到α的距离为 ,则P. Q两点之间距离的最小值为 ;
,则P. Q两点之间距离的最小值为 ; 边长为
边长为 ,角
,角 ,沿
,沿 将
将 折起,使二面角
折起,使二面角 为
为 ,则折起后
,则折起后 、
、 之间的距离是 .
之间的距离是 . ,
, ,
,
 是平面,
是平面, 是直线,给出下列命题,其中正确的命题的个数是( )
是直线,给出下列命题,其中正确的命题的个数是( ) ,则
,则
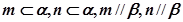 ,则
,则
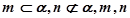 是异面直线,那么
是异面直线,那么 与
与 相交
相交 ,且
,且 ,则
,则 且
且 .
.