题目内容
（本题满分16分）已知数列
中，
，
，且
．（Ⅰ）设
，证明
是等比数列；
（Ⅱ）求数列的通项公式；
（Ⅲ）若
是
与
的等差中项，求
的值，并证明：对任意的
，
是
与
的等差中项．
解析：（Ⅰ）证明：由题设
，得
，
即
．
又
，
，所以
是首项为1，公比为
的等比数列．
（Ⅱ）解：由（Ⅰ），
，
，
……
．
将以上各式相加，得
．所以当
时，
上式对
显然成立．
（Ⅲ）解：由（Ⅱ），当
时，显然
不是
与
的等差中项，故
．
由
可得
，由得
， ①
整理得
，解得
或
（舍去）．于是
．
另一方面，
，
．
由①可得
．
所以对任意的
，
是
与
的等差中项．
练习册系列答案
相关题目
，且对任意
，有
.
；
在区间（0，1）上为单调函数，求实
数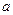
的取值范围.
的零点个数？(提示
)
为实常数）．
时，求函数
在
上的最小值；
在区间
上有解，求实数
的取值范围；
）
：
的离心率为
，
分别为椭圆
为椭圆上任意一点，以
为半径作圆
有公共点时，求△
面积的最大值．
是定义在
上的偶函数，且当
时，
。
及
的值；
上的解析式；
的方程
有四个不同的实数解，求实数
的取值范围。