题目内容
从0，1，2，3，4，5这6个数字中任意取4个数字组成一个没有重复数字且能被3整除的四位数，这样的四位数有______个．
根据题意，要求四位数能被3整除，
则选出的四个数字有5种情况，①1，2，4，5；②0，3，4，5；③0，2，3，4；④0，1，3，5；⑤0，1，2，3；
①时，共可以组成A44=24个四位数；
②时，0不能在首位，此时可以组成3×A33=3×3×2×1=18个四位数，
同理，③、④、⑤时，都可以组成18个四位数，
则这样的四位数共24+4×18=96个；
故答案为：96．
则选出的四个数字有5种情况，①1，2，4，5；②0，3，4，5；③0，2，3，4；④0，1，3，5；⑤0，1，2，3；
①时，共可以组成A44=24个四位数；
②时，0不能在首位，此时可以组成3×A33=3×3×2×1=18个四位数，
同理，③、④、⑤时，都可以组成18个四位数，
则这样的四位数共24+4×18=96个；
故答案为：96．
练习册系列答案
相关题目
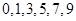这六个数字组成_____个没有重复数字的六位奇数.(数字作答)
