题目内容
 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x(2-x).
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x(2-x).(1)画出偶函数f(x)的图象;
(2)根据图象,写出f(x)的单调递减区间和单调递增区间;同时写出函数的值域;
(3)求函数f(x)的解析式.
分析:(1)根据偶函数的对称性即可画出偶函数f(x)的图象;
(2)根据图象,即可得到f(x)的单调递减区间和单调递增区间;同时写出函数的值域;
(3)根据函数的奇偶性的性质求函数f(x)的解析式.
(2)根据图象,即可得到f(x)的单调递减区间和单调递增区间;同时写出函数的值域;
(3)根据函数的奇偶性的性质求函数f(x)的解析式.
解答:解:(1)偶函数f(x)的图象如右图所示:
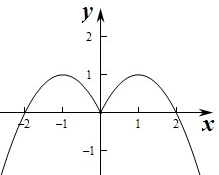
(2)由图得函数f(x)的单调递减区间是(-1,0),(1,+∞).
f(x)的单调递增区间是(-∞,-1),(0,1).
值域为{y|y≤1}.
(注意:将两个区间“并”起来,没分;-1,0,1处写为“闭”的形式,不扣分)
(3)设x<0,则-x>0,f(-x)=-x(2+x),
∵f(x)是偶函数,
∴f(-x)=f(x),
∴f(x)=-x(2+x),
∴函数f(x)的解析式为f(x)=
.

(2)由图得函数f(x)的单调递减区间是(-1,0),(1,+∞).
f(x)的单调递增区间是(-∞,-1),(0,1).
值域为{y|y≤1}.
(注意:将两个区间“并”起来,没分;-1,0,1处写为“闭”的形式,不扣分)
(3)设x<0,则-x>0,f(-x)=-x(2+x),
∵f(x)是偶函数,
∴f(-x)=f(x),
∴f(x)=-x(2+x),
∴函数f(x)的解析式为f(x)=
|
点评:本题主要考查函数奇偶性的应用,利用偶函数的对称性是解决本题的关键,综合考查函数性质的综合应用.

练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+