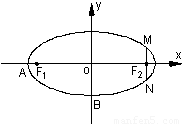
题目内容
已知椭圆 :
:
 的左、右焦点分别为
的左、右焦点分别为 离心率
离心率
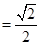 ,点
,点 在且椭圆E上,
在且椭圆E上,
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过点 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆 于
于 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点 ,求点
,求点 横坐标的取值范围.
横坐标的取值范围.
(Ⅲ)试用 表示
表示 的面积,并求
的面积,并求 面积的最大值
面积的最大值
【答案】
(Ⅰ)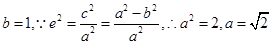 ,
,
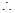 椭圆E的方程为
椭圆E的方程为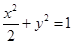 -------------------4分
-------------------4分
(Ⅱ)设直线AB的方程为y=k(x-1)(k≠0),
代入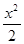 +y2=1,整理得(1+2k2)x2-4k2x+2k2-2=0.
+y2=1,整理得(1+2k2)x2-4k2x+2k2-2=0.
∵直线AB过椭圆的右焦点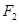 ,
,
∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),则x1+x1=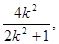
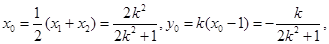 ---------------6分
---------------6分
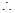
 AB垂直平分线NG的方程为
AB垂直平分线NG的方程为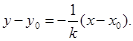 令y=0,得
令y=0,得
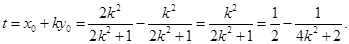 ----------------8分
----------------8分
∵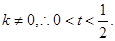 ∴的取值范围为
∴的取值范围为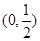 . -------10分
. -------10分
(Ⅲ)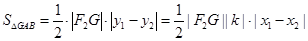 .
.
而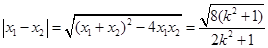 ,
,
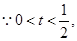 由
由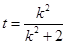 ,
,
可得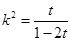 ,
,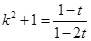 ,
,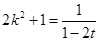 .
.
所以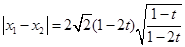 .
.
又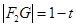 ,所以
,所以
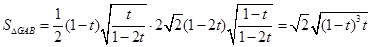 (
(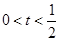 ).---12
).---12
设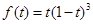 ,则
,则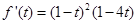 .
.
可知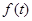 在区间
在区间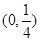 单调递增,在区间
单调递增,在区间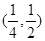 单调递减.
单调递减.
所以,当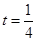 时,
时,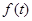 有最大值
有最大值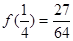 .
.
所以,当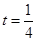 时,△
时,△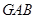 的面积有最大值
的面积有最大值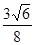 .
.
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:

 的方程为
的方程为  ,双曲线
,双曲线 的左、右焦
的左、右焦 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求 的范围。
的范围。 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的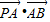 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.