题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
又当 当 上式对 ∴ |
(2) |
由已知 由 ∴ 当 由 即 总之,存在整数 |
(3) |
将不等式变形并把
设 ∴ ∴ 又∵ ∴ ∴ ∴ |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
| |||||||||||
 ,问是否存在k∈N+使f(k+27)=4f(k)成立?若存在,求出k的值;若不存在,说明理由
,问是否存在k∈N+使f(k+27)=4f(k)成立?若存在,求出k的值;若不存在,说明理由 恒成立,求正数a的取值范围.
恒成立,求正数a的取值范围.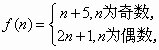 ∴当
∴当