题目内容
给出下列命题:
①若数列{an}的前n项和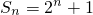 ,则数列{an}为等比数列;
,则数列{an}为等比数列;
②在△ABC中,如果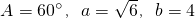 ,那么满足条件的△ABC有两解;
,那么满足条件的△ABC有两解;
③设函数f(x)=x|x-a|+b,则函数f(x)为奇函数的充要条件是a2+b2=0;
④设直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π),则M中的直线所能围成的正三角形面积都相等.
其中真命题的序号是________.
③
分析:本题需逐个判断:选项①的数列从第2项起成等比数列;选项②三角形无解;选项③,通过奇函数的定义可得结论;选项④,通过三角换元可知,直线为定圆的切线,画图可得M中的直线所能围成的正三角形面积不一定相等.
解答: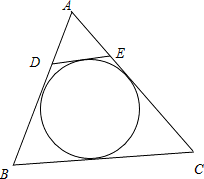 解:选项①,当n=1时,可得a1=3,当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,显然n=1时式子不符合,故数列{an}不是等比数列;
解:选项①,当n=1时,可得a1=3,当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,显然n=1时式子不符合,故数列{an}不是等比数列;
选项②,∵a= <bsinA=
<bsinA= ,故满足条件的三角形无解,故错误;
,故满足条件的三角形无解,故错误;
选项③,函数f(x)=x|x-a|+b的定义域为R,故函数f(x)为奇函数的充要条件是f(-x)+f(x)=0,
即x|x-a|+b-x|x+a|+b=0,故x(|x-a|-|x+a|)+2b=0,只能a,b同时为0,即a2+b2=0,故正确;
选项④,由直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π),可令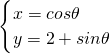
消去θ可得 x2+(y-2)2=1,故 直线系M表示圆 x2+(y-2)2=1 的切线的集合,如图中等边三角形ABC和 ADE面积不相等,故不正确.
故答案为:③
点评:本题为命题真假的判断,涉及数列,解三角形,函数的奇偶性以及三角换元,属中档题.
分析:本题需逐个判断:选项①的数列从第2项起成等比数列;选项②三角形无解;选项③,通过奇函数的定义可得结论;选项④,通过三角换元可知,直线为定圆的切线,画图可得M中的直线所能围成的正三角形面积不一定相等.
解答:
 解:选项①,当n=1时,可得a1=3,当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,显然n=1时式子不符合,故数列{an}不是等比数列;
解:选项①,当n=1时,可得a1=3,当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,显然n=1时式子不符合,故数列{an}不是等比数列;选项②,∵a=
 <bsinA=
<bsinA= ,故满足条件的三角形无解,故错误;
,故满足条件的三角形无解,故错误;选项③,函数f(x)=x|x-a|+b的定义域为R,故函数f(x)为奇函数的充要条件是f(-x)+f(x)=0,
即x|x-a|+b-x|x+a|+b=0,故x(|x-a|-|x+a|)+2b=0,只能a,b同时为0,即a2+b2=0,故正确;
选项④,由直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π),可令
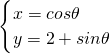
消去θ可得 x2+(y-2)2=1,故 直线系M表示圆 x2+(y-2)2=1 的切线的集合,如图中等边三角形ABC和 ADE面积不相等,故不正确.
故答案为:③
点评:本题为命题真假的判断,涉及数列,解三角形,函数的奇偶性以及三角换元,属中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目