题目内容

现给出下列命题：
①若p，q是两个简单命题，则“p且q为真”是“p或q为真”的必要不充分条件；
②若椭圆
x2
16
+
y2
25
=1的两个焦点为F1，F2，且弦AB过点F1，则△ABF2的周长为16；
③过点（0，2）与抛物线y2=-5x仅有一个公共点的直线有3条；
④导数为0的点一定是函数的极值点．
其中正确的结论的序号是
 
（要求写出所有正确结论的序号）．
分析：根据复合命题的真假性法则判断出命题①错误；由椭圆的定义得出△ABF2的周长为4a，再由椭圆的标准方程求出a的值即可判断出命题②错误；通过画出图象判断出命题③正确；举出特殊函数作为反例说明④错误．
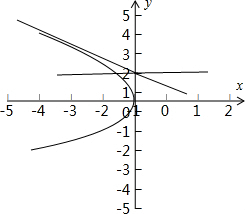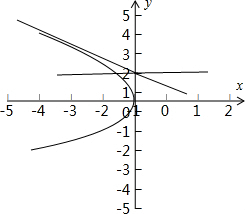解答：精英家教网解：命题①：p∧q为真说明p和q都为真，而p∨q为真说明p或q有一个为真，
∴p∧q⇒p∨q，而反之不行．
∴p∧q为真”是“p∨q为真的充分不必要条件，命题①错误；
命题②：椭圆是平面上到两定点的距离之和为常值的点之轨迹，故无论A和B在椭圆的那个位置上，
由定义知AF1+AF2=2a，BF1+BF2=2a 其中2a为长轴的距离，由题意知a=5，
故△ABF2的周长为AF1+AF2+BF1+BF2=4a=20，命题②错误； 
命题③：如右图：可知过点（0，2）与此抛物线有一个公共点的有3条，如图有两条，还有一条就是y轴，∴命题③正确；
命题④：可以举反例出来，f（x）=x3的导数在0点是0，但函数在0点并不是极值点，命题④错误．
故答案为：③．
点评：本题考查了命题的真假性判断，复合命题的真假性法则，椭圆的定义和抛物线的图象，以及函数极值等问题，考查了的范围广，需要熟练掌握基础知识以及应用．
练习册系列答案
相关题目
设函数f（x）的定义域为D，若存在非零数l使得对于任意x∈M（M⊆D）有x+l∈D且f（x+l）≥f（x），则称f（x）为M上的l高调函数．现给出下列命题：
①函数f（x）=(
12
)x为R上的1高调函数；
②函数f（x）=sin2x为R上的π高调函数
③如果定义域为[1，+∞）的函数f（x）=x2为[-1，+∞）上m高调函数，那么实数m的取值范围是[2，+∞）其中正确的命题是
 
．（写出所有正确命题的序号）
（2013•茂名二模）设函数f（x）的定义域为D，若存在非零实数l使得对于任意x∈M（M⊆D），有x+l∈D，且f（x+l）≥f（x），则称f（x）为M上的高调函数．现给出下列命题：
①函数f（x）=log 
1
2
x为（0，+∞）上的高调函数；
②函数f（x）=sinx为R上的高调函数；
③如果定义域为[-1，+∞）的函数f（x）=x2为[-1，+∞）上的高调函数，那么实数m的取值范围是[2，+∞）；
其中正确的命题的个数是（　　）
（2012•泸州一模）设函数f（x）的定义域为D，若存在非零实数l使得对于任意x∈M（M⊆D），有x+l∈M，且f（x+l）≥f（x），则称f（x）为M上的l高调函数．现给出下列命题：
①函数f(x)=(
12
)x为R上的1高调函数；
②函数f（x）=lgx为（0，+∞）上的m（m＞0）高调函数；
③函数f（x）=sin2x为R上的π高调函数；
④若函数f（x）=x2为[-1，+∞）上的m高调函数，那么实数m的取值范围是[2，+∞）．
其中正确命题的序号是
①②③④
①②③④
（写出所有正确命题的序号）．
（2011•遂宁二模）设函数f（x）的定义域为D，若存在非零实数，使得对于任意x∈M（M⊆D），有x+l∈D，f（x+l）≥f（x），则称f（x）为M上的l高调函数，现给出下列命题：
①函数f(x)=(
12
)x为R上的1高调函数；
②函数f （x）=sin 2x为R上的高调函数；
③如果定义域是[-1，+∞）的函数f（x）=x2为[-1，+∞）上的m高调函数，那么实数m的取值范围是[2，+∞）；
④如果定义域为R的函教f （x）是奇函数，当x≥0时，f（x）=|x-a2|-a2，且f（x）为R上的4高调函数，那么实数a的取值范围是[一1，1]．
其中正确的命题是
②③④
②③④
 （写出所有正确命题的序号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网