题目内容
【题目】如图,在棱长为1的正方体![]() 中,动点
中,动点![]() 在线段
在线段![]() 上运动,且有
上运动,且有![]() .
.
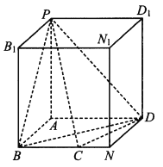
(1)若![]() ,求证:
,求证:![]() ;
;
(2)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)当![]() 时,
时,![]() 与
与![]() 重合,连接
重合,连接![]() ,可得
,可得![]() ,再由正方体特征可证得
,再由正方体特征可证得![]() ,即可证得
,即可证得![]() 平面
平面![]() ,问题得证。
,问题得证。
(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系.分别求出平面
轴建立空间直角坐标系.分别求出平面![]() 的一个法向量
的一个法向量![]() 及平面
及平面![]() 的一个法向量
的一个法向量![]() ,利用向量夹角的坐标表示列方程即可求得
,利用向量夹角的坐标表示列方程即可求得![]() ,问题得解。
,问题得解。
(1)当![]() 时,
时,![]() 与
与![]() 重合,连接
重合,连接![]() ,
,
则在正方形![]() 中,
中,![]() .
.
又在正方体中![]() 底面
底面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() .
.
![]() ,所以
,所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() ,也即
,也即![]() .
.
(2)依题意,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
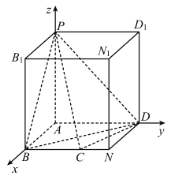
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则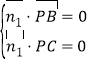 ,即
,即![]() ,
,
取![]() 得
得![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则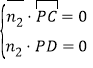 ,即
,即![]() ,
,
取![]() 得
得![]() .
.
所以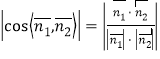
![]() ,
,
解得![]() 或
或![]() .
.
因为![]() ,所以
,所以![]() .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人![]() 次数学考试的成绩,统计结果如下表:
次数学考试的成绩,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若答对,则可参加复赛,否则被淘汰.
道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若至少答对其中
道,若至少答对其中![]() 道,则可参加复赛,否则被润汰.
道,则可参加复赛,否则被润汰.
已知学生甲、乙都只会![]() 道备选题中的
道备选题中的![]() 道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.