题目内容
复数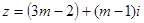 ,
,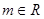 .
.
(1) 为何值时,
为何值时, 是纯虚数?
是纯虚数? 取什么值时,
取什么值时, 在复平面内对应的点位于第四象限?
在复平面内对应的点位于第四象限?
(2)若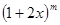 (
( )的展开式第3项系数为40,求此时
)的展开式第3项系数为40,求此时 的值及对应的复数
的值及对应的复数 的值.
的值.
(1)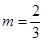 ,
,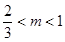 ;(2)
;(2)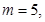
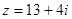 .
.
解析试题分析:(1)对于复数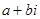 可知当
可知当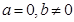 时为纯虚数,在复平面内对应的点为
时为纯虚数,在复平面内对应的点为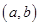 ,则有
,则有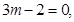 且
且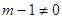 时
时 是纯虚数,当
是纯虚数,当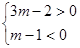 时,
时, 在复平面内对应的点位于第四象限.(2)由二项展开式
在复平面内对应的点位于第四象限.(2)由二项展开式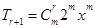 ,可知展开式第3项
,可知展开式第3项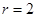 时,系数为
时,系数为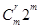 =40,可得m .
=40,可得m .
解:(1)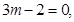 且
且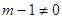 时,即
时,即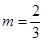 时,
时, 是纯虚数,
是纯虚数, 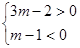 解得
解得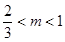 ,此时
,此时 复平面内对应的点位于第四象限.
复平面内对应的点位于第四象限.
(2)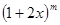 的展开式第3项系数为
的展开式第3项系数为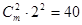 ,化简得
,化简得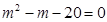 ,
,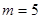 或
或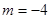 (负,舍去),
(负,舍去),
∴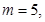 此时
此时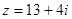 .
.
考点:复数的概念和复数的几何意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,且
,且 为虚数单位,则
为虚数单位,则 的最小值是
的最小值是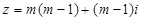 .
.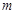 为何值时,复数
为何值时,复数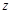 为纯虚数?
为纯虚数? ,计算复数
,计算复数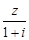 .
. 是复数,
是复数,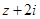 、
、 均为实数(
均为实数( 为虚数单位),且复数
为虚数单位),且复数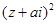 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数 的取值范围.
的取值范围.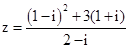 .
.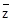 ;
;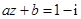 ,求实数
,求实数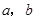 的值.
的值.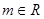 ,复数
,复数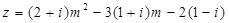 ,
,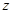 的代数形式;
的代数形式;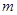 为何值时,
为何值时,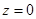 ?当
?当 在复平面上对应的点在第 象限。
在复平面上对应的点在第 象限。 =(a+2z)2.
=(a+2z)2.