题目内容
如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成”函数。给出下列函数:
① ②
② ;
;
③ ; ④
; ④ 其中“互为生成”函数的是( )
其中“互为生成”函数的是( )
| A.①② | B.②③ | C.③④ | D.①④ |
D
解析试题分析:根据已知条件可知①f(x)=sinx+cosx=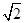 sin(x+
sin(x+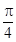 );
);
②f(x)= 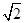 (sinx+cosx)=2sin(x+
(sinx+cosx)=2sin(x+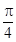 ).
).
③f(x)=sinx;④f(x)= 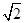 sinx+
sinx+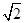
显然只有①④,可以经过平移两个函数的图象能够重合,
②③两个函数之间,与①④要想重合,不仅需要平移,还必须有伸缩变换才能实现.
故选D
考点:本题是基础题,实质考查函数图象的平移和伸缩变换问题,只要掌握基本知识,领会新定义的实质,不难解决问题.
点评:解决该试题的关键是化简函数①②,使之成为一个角的一个三角函数的形式,观察①②③④,不难推出满足题意的函数,即可得到选项.

练习册系列答案
相关题目
设函数 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A.把 的图象向左平移 的图象向左平移 个单位,得到一个偶函数的图象 个单位,得到一个偶函数的图象 |
B. 的图象关于点 的图象关于点 对称 对称 |
C. 的图象关于直线 的图象关于直线 对称 对称 |
D. 的最小正周期为 的最小正周期为 ,且在 ,且在 上为增函数 上为增函数 |
如图,为了得到这个函数的图象,只要将 的图象上所有的点( )
的图象上所有的点( )
A.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
B.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
 为第四象限角,
为第四象限角, ,则
,则 =
=
A. | B. | C. | D. |
下列函数中,最小正周期为 ,且图像关于直线
,且图像关于直线 对称的是( )
对称的是( )
A. | B. |
C. | D. |
函数 的最小正周期等于 ( )
的最小正周期等于 ( )
A. | B.2 | C. | D. |
 的值为
的值为
A. | B. | C. | D. |
把函数y=sin(x+ )图像上各点的横坐标缩短为原来的
)图像上各点的横坐标缩短为原来的 倍(纵坐标不变),再将图像向右平移
倍(纵坐标不变),再将图像向右平移 个单位,那么所得图像的一条对称轴方程为
个单位,那么所得图像的一条对称轴方程为
A.x=- | B.x =- |
C.x = | D.x = |
将函数 的图象向右平移
的图象向右平移 个单位, 再向上平移1个单位,所得图象的函数解析式是( )
个单位, 再向上平移1个单位,所得图象的函数解析式是( )
A. | B. |
C. | D. |