题目内容
设函数 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A.把 的图象向左平移 的图象向左平移 个单位,得到一个偶函数的图象 个单位,得到一个偶函数的图象 |
B. 的图象关于点 的图象关于点 对称 对称 |
C. 的图象关于直线 的图象关于直线 对称 对称 |
D. 的最小正周期为 的最小正周期为 ,且在 ,且在 上为增函数 上为增函数 |
A
解析试题分析:根据正弦函数的性质可知f(x)=sin(2x+ )的对称轴为2x+
)的对称轴为2x+ =kπ+
=kπ+ (k∈Z),即x=
(k∈Z),即x=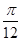 +
+ (k∈Z)∴直线x=
(k∈Z)∴直线x= 不是函数f(x)的对称轴,结论(3)错误
不是函数f(x)的对称轴,结论(3)错误
根据正弦函数的性质可知f(x)=sin(2x+ )的对称中心横坐标为2x+
)的对称中心横坐标为2x+ =kπ,即x=
=kπ,即x= -
-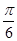 ,∴点(
,∴点(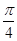 ,0)不是函数的对称中心.结论(2)错误.
,0)不是函数的对称中心.结论(2)错误.
f(x)的图象向左平移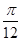 个单位,得f(x)=sin(2x+
个单位,得f(x)=sin(2x+ )
)
)=cos2x,为偶函数,∴结论(1)正确.
f(x)的最小正周期为π,且2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ 时,即kπ-
时,即kπ-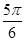 ≤x≤kπ+
≤x≤kπ+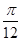
函数单调增,∴结论(4)不正确.故答案为A
考点:本题主要考查了三角函数的周期性和求法,三角函数的单调性和对称性,属于中档题
点评:解决该试题的关键是利用正弦函数的单调性,对称性和三角函数图象的平移法则,对四个结论逐一验证,答案可得.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 与
与 是
是 相邻的两条对称轴,化简
相邻的两条对称轴,化简 为( )
为( )
| A.1 | B.2 | C. | D.0 |
下列命题正确的是( ).
| A.终边相同的角都相等 | B.钝角比第三象限角小 |
| C.第一象限角都是锐角 | D.锐角都是第一象限角 |
要得到 的图象,只需将
的图象,只需将 的图象( ).
的图象( ).
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
把-495°表示成k×360°+θ(k∈Z)的形式,则θ可以是( )
| A.-135° | B.45° | C.-225° | D.135° |
函数 的定义域为
的定义域为 ,值域为
,值域为 ,则
,则 的最大值与最小值之和为
的最大值与最小值之和为
A. | B. | C. | D. |
二面角 的平面角是锐角,点C
的平面角是锐角,点C 且点C不在棱AB上,D是C在平面
且点C不在棱AB上,D是C在平面 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
| A.∠CEB>∠DEB | B.∠CEB=∠DEB |
| C.∠CEB<∠DEB | D.∠CEB与∠DEB的大小关系不能确定 |
 )图像上的一段,则( )
)图像上的一段,则( ) ,φ=
,φ=

 ②
② ;
; ; ④
; ④ 其中“互为生成”函数的是( )
其中“互为生成”函数的是( )