题目内容
(本小题满分12分)设函数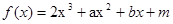 的导函数为
的导函数为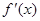 ,若函数
,若函数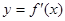 的图像关于直线
的图像关于直线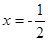 对称,且
对称,且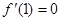 .
.
(1)求实数a、b的值
(2)若函数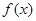 恰有三个零点,求实数
恰有三个零点,求实数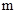 的取值范围。
的取值范围。
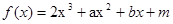 的导函数为
的导函数为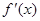 ,若函数
,若函数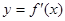 的图像关于直线
的图像关于直线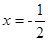 对称,且
对称,且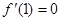 .
.(1)求实数a、b的值
(2)若函数
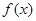 恰有三个零点,求实数
恰有三个零点,求实数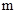 的取值范围。
的取值范围。(1)b=-12;(2)

本试题主要是考查了导数在研究函数中的运用。
(1)因为 ,则其对称轴为
,则其对称轴为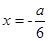 ,由已知可得
,由已知可得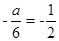 ,所以a=3,同时由
,所以a=3,同时由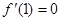 可得,b=-12
可得,b=-12
(2)由(1)得: ,若函数
,若函数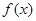 恰有三个零点,则必有极大值大于零,极小值小于零,得到参数m的范围。
恰有三个零点,则必有极大值大于零,极小值小于零,得到参数m的范围。
所以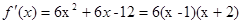
解:(1)
则其对称轴为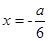 ,由已知可得
,由已知可得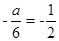 ,所以a=3
,所以a=3
又由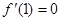 可得,b=-12 ………………5分
可得,b=-12 ………………5分
(2)由(1)得:
所以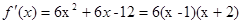
当 时,
时, ,
,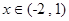 时,
时,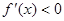 ,
,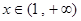 时,
时,
故函数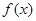 在
在 和
和 上递增,在
上递增,在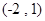 上递减
上递减
所以函数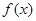 的极大值为
的极大值为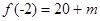 ,极小值为
,极小值为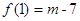 ………………10分
………………10分
而函数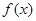 恰有三个零点,故必有
恰有三个零点,故必有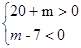 ,解得:
,解得: …………12分
…………12分
(1)因为
 ,则其对称轴为
,则其对称轴为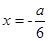 ,由已知可得
,由已知可得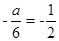 ,所以a=3,同时由
,所以a=3,同时由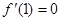 可得,b=-12
可得,b=-12(2)由(1)得:
 ,若函数
,若函数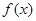 恰有三个零点,则必有极大值大于零,极小值小于零,得到参数m的范围。
恰有三个零点,则必有极大值大于零,极小值小于零,得到参数m的范围。所以
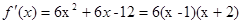
解:(1)

则其对称轴为
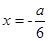 ,由已知可得
,由已知可得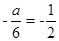 ,所以a=3
,所以a=3又由
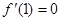 可得,b=-12 ………………5分
可得,b=-12 ………………5分 (2)由(1)得:

所以
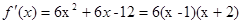
当
 时,
时, ,
,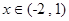 时,
时,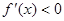 ,
,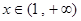 时,
时,
故函数
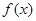 在
在 和
和 上递增,在
上递增,在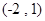 上递减
上递减所以函数
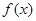 的极大值为
的极大值为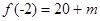 ,极小值为
,极小值为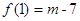 ………………10分
………………10分 而函数
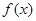 恰有三个零点,故必有
恰有三个零点,故必有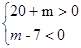 ,解得:
,解得: …………12分
…………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
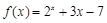 的一个零点,某同学利用计算器得到自变量
的一个零点,某同学利用计算器得到自变量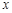 和函数
和函数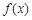 的部分对应值,如表所示:
的部分对应值,如表所示: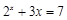 的近似解(精确到0.1)可取为
的近似解(精确到0.1)可取为 上的奇函数
上的奇函数 满足
满足 ,且在区间
,且在区间 上是增函数.若方程
上是增函数.若方程 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ______
______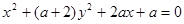 表示一个圆
表示一个圆 则( )
则( )







 ( )
( )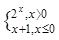 ,若f(a)+f(1)=0,则实数a的值等于 .
,若f(a)+f(1)=0,则实数a的值等于 . ,关于
,关于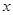 的方程
的方程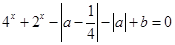 总有实根,则实数
总有实根,则实数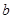 的取值范围是 .
的取值范围是 . 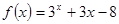 ,用二分法求方程
,用二分法求方程 内近似解的过中 得
内近似解的过中 得 则方程的根落在区间( )
则方程的根落在区间( ) 满足
满足 ,且在
,且在 时,
时, ,则关于
,则关于 的方程
的方程 在
在 上根的个数是( )
上根的个数是( )