题目内容
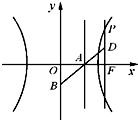 如图,已知双曲线
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| OD |
| OF |
| OP |
(Ⅰ)求双曲线的离心率;
(Ⅱ)若a=2,过点(0,-2)的直线l交该双曲线于不同两点M、N,求
| OM |
| ON |
分析:(Ⅰ)根据题意可分别表示出点A、B、P、F的坐标,则直线AB的方程可表示出,把x=c代入求得y,则d点坐标可得,根据2
=
+
,可知2(c,
)=(c,0)+(c,
),求得a和b的关系,进而求得a和c的关系,则双曲线离心率可得.
(Ⅱ)根据(1)中a和b的关系式根据a可求得b,则双曲线方程可得,设出直线l的方程与双曲线方程联立消去y,根据根据判别式求得k的范围,根据韦达定理表示出x1+x2和x1x2的表达式,进而表示出
•
,根据k的范围确定其取值范围.
| OD |
| OF |
| OP |
| b3 |
| a2 |
| b2 |
| a |
(Ⅱ)根据(1)中a和b的关系式根据a可求得b,则双曲线方程可得,设出直线l的方程与双曲线方程联立消去y,根据根据判别式求得k的范围,根据韦达定理表示出x1+x2和x1x2的表达式,进而表示出
| OM |
| ON |
解答:解:(Ⅰ)点A、B、P、F的坐标分别为A(
,0),B(0,-b),P(c,
),F(c,0),
直线AB的方程为
+
=1,令x=c,则y=
,知D(c,
),
∵2
=
+
,∴2(c,
)=(c,0)+(c,
),则
=
,∴a=2b,
∴e=
=
=
=
.
(Ⅱ)∵a=2,∴b=1,双曲线的方程是
-y2=1,知直线l的斜率存在,
设直线l方程为y=kx-2,联立方程组
得(1-4k2)x2+16kx-20=0,设M(x1,y1),N(x2,y2),
由
解得k2<
且k2≠
.
∴x1+x2=
,x1x2=
.
•
=x1x2+y1y2=x1x2+(kx1-2)(kx2-2)=(1+k2)x1x2-2k(x1+x2)+4=
-
+4=
=1+
,
∵0≤k2<
且k2≠
,∴
∈(-∞,-17]∪(
,+∞),
则
•
的范围是(-∞,-16]∪(
,+∞).
| a2 |
| c |
| b2 |
| a |
直线AB的方程为
| x | ||
|
| y |
| -b |
| b3 |
| a2 |
| b3 |
| a2 |
∵2
| OD |
| OF |
| OP |
| b3 |
| a2 |
| b2 |
| a |
| 2b3 |
| a2 |
| b2 |
| a |
∴e=
| c |
| a |
| ||
| a |
1+(
|
| ||
| 2 |
(Ⅱ)∵a=2,∴b=1,双曲线的方程是
| x2 |
| 4 |
设直线l方程为y=kx-2,联立方程组
|
得(1-4k2)x2+16kx-20=0,设M(x1,y1),N(x2,y2),
由
|
| 5 |
| 4 |
| 1 |
| 4 |
∴x1+x2=
| 16k |
| 4k2-1 |
| 20 |
| 4k2-1 |
| OM |
| ON |
| 20(1+k2) |
| 4k2-1 |
| 32k2 |
| 4k2-1 |
| 4k2+16 |
| 4k2-1 |
| 17 |
| 4k2-1 |
∵0≤k2<
| 5 |
| 4 |
| 1 |
| 4 |
| 17 |
| 4k2-1 |
| 17 |
| 4 |
则
| OM |
| ON |
| 21 |
| 4 |
点评:本题主要考查了双曲线的简单性质.考查了直线与圆锥曲线的位置关系.综合考查了学生基础知识的掌握和理解.

练习册系列答案
相关题目
 如图,已知双曲线x2-
如图,已知双曲线x2-| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 (2013•上海)如图,已知双曲线C1:
(2013•上海)如图,已知双曲线C1: ,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
 内的点都不是“C1﹣C2型点”
内的点都不是“C1﹣C2型点”