题目内容
如图,已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2)。
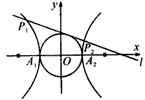
(1)求k的取值范围,并求x2-x1的最小值;
(2)记直线P1A1的斜率为k1,直线P2A2的斜率为k2,那么,k1·k2是定值吗?证明你的结论。
(2)记直线P1A1的斜率为k1,直线P2A2的斜率为k2,那么,k1·k2是定值吗?证明你的结论。
解:(1)∵l与圆相切
∴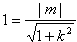
∴m2=1+k2
由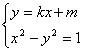 得(1-k2)x2-2mkx-(m2+1)=0
得(1-k2)x2-2mkx-(m2+1)=0
∴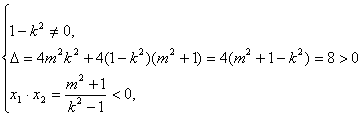
∴k2<1,
∴-1<k<1
故k的取值范围为(-1,1)
由于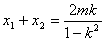
所以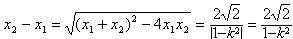
∵0≤k2<1
∴当k2=0时,x2-x1取最小值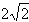 。
。
(2)由已知可得A1,A2的坐标分别为(-1,0),(1,0)
∴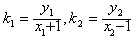
∴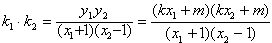
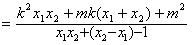
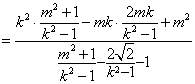
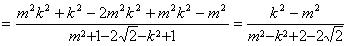
由(1)得m2-k2=1
∴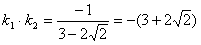 为定值。
为定值。
∴
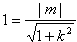
∴m2=1+k2
由
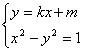 得(1-k2)x2-2mkx-(m2+1)=0
得(1-k2)x2-2mkx-(m2+1)=0∴
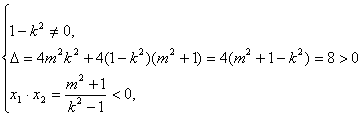
∴k2<1,
∴-1<k<1
故k的取值范围为(-1,1)
由于
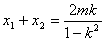
所以
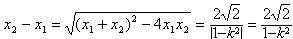
∵0≤k2<1
∴当k2=0时,x2-x1取最小值
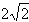 。
。(2)由已知可得A1,A2的坐标分别为(-1,0),(1,0)
∴
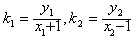
∴
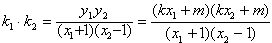
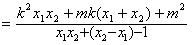
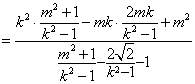
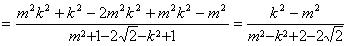
由(1)得m2-k2=1
∴
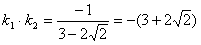 为定值。
为定值。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
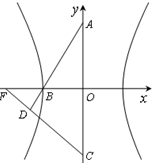 如图,已知双曲线x2-
如图,已知双曲线x2-| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 (2013•上海)如图,已知双曲线C1:
(2013•上海)如图,已知双曲线C1: ,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
 内的点都不是“C1﹣C2型点”
内的点都不是“C1﹣C2型点”