题目内容
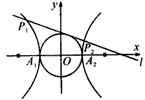
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求证直线PQ与双曲线的一条渐近线垂直.
(Ⅱ)若M为PF2的中点,O为坐标原点,|OM|-|MT|=1,|PQ|=λ|AB|,求实数λ的取值范围.
分析:(Ⅰ)先根据双曲线的性质表示出渐近线方程,设出PQ的方程,根据与圆相切求得圆心到直线的距离为半径求得k的表达式,进而把两渐近线的斜率相乘即可.
(Ⅱ)设出PF的直线方程与双曲线方程联立,消去y,利用韦达定理表示出x1+x2和x1x2,进而利用弦长公式表示出|PQ|,同时依题意可知|OM|=
|PF1|,|F2M|=
|PF2|,推断出|F2M|-|MT|=a+1,进而求得b和a的关系式,然后利用|PQ|和|AB|,表示出λ,利用换元法令t=2a+1,利用函数的单调性求得λ的范围.
(Ⅱ)设出PF的直线方程与双曲线方程联立,消去y,利用韦达定理表示出x1+x2和x1x2,进而利用弦长公式表示出|PQ|,同时依题意可知|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(Ⅰ)双曲线
-
=1(b>a>0)的渐近线为y=±
x,
设直线PQ的方程为y=k(x-c),(不妨设k<0),由于与圆x2+y2=a2相切,
∴
=a,即k2=
,直线PQ的斜率k=-
,
因为一三象限的渐近线为
,-
•
=-1.
所以直线PQ与双曲线的一条渐近线垂直;
(Ⅱ)
得(b2-a2k2)x2+2a2k2cx-a2k2c2-a2b2=0,
设P(x1,y1),Q(x2,y2),
则
,
所以|PQ|=
=
=
,
因为|OM|=
|PF1|,|F2M|=
|PF2|,|F2M|-|OM|=
(|PF2|-|PF1|)=a,|OM|-|MT|=1,
代入上式得|F2M|-|MT|=a+1,
又|F2M|-|MT|=|F2T|=
=b,
所以b=a+1.
因为|AB|=2a,|PQ|=
,
λ=
=
=
+1,
令t=2a+1,则a=
,t∈[3,5],λ=
[t+
-2]+1,
因为t+
在[3,5]为增函数,所以λ∈[
,
].
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
设直线PQ的方程为y=k(x-c),(不妨设k<0),由于与圆x2+y2=a2相切,
∴
| |kc| | ||
|
| a2 |
| b2 |
| a |
| b |
因为一三象限的渐近线为
| b |
| a |
| a |
| b |
| b |
| a |
所以直线PQ与双曲线的一条渐近线垂直;
(Ⅱ)
|
得(b2-a2k2)x2+2a2k2cx-a2k2c2-a2b2=0,
设P(x1,y1),Q(x2,y2),
则
|
所以|PQ|=
| (1+k2)[(x1+x2)2-4x1x2] |
=
| 2ab2(1+k2) |
| |b2-a2k2| |
=
| 2ab2 |
| b2-a2 |
因为|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入上式得|F2M|-|MT|=a+1,
又|F2M|-|MT|=|F2T|=
| c2-a2 |
所以b=a+1.
因为|AB|=2a,|PQ|=
| 2ab2 |
| b2-a2 |
λ=
| b2 |
| b2-a2 |
| (a+1)2 |
| 2a+1 |
| a2 |
| 2a+1 |
令t=2a+1,则a=
| t-1 |
| 2 |
| 1 |
| 4 |
| 1 |
| t |
因为t+
| 1 |
| t |
| 4 |
| 3 |
| 9 |
| 5 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生对解析几何学知识的综合运用.

练习册系列答案
相关题目
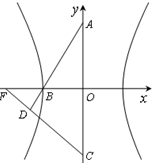 如图,已知双曲线x2-
如图,已知双曲线x2-| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 (2013•上海)如图,已知双曲线C1:
(2013•上海)如图,已知双曲线C1: ,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
 内的点都不是“C1﹣C2型点”
内的点都不是“C1﹣C2型点”