题目内容
设数列{an}满足a1＋2a2＝3，且对任意的n∈N*，点列{Pn(n，an)}恒满足PnPn＋1＝(1,2)，则数列{an}的前n项和Sn为________．
n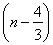
【解析】设Pn＋1(n＋1，an＋1)，则PnPn＋1＝(1，an＋1－an)＝(1,2)，即an＋1－an＝2，所以数列{an}是以2为公差的等差数列．又因为a1＋2a2＝3，所以a1＝－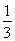
，所以Sn＝n.
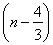练习册系列答案
相关题目
题目内容
设数列{an}满足a1＋2a2＝3，且对任意的n∈N*，点列{Pn(n，an)}恒满足PnPn＋1＝(1,2)，则数列{an}的前n项和Sn为________．
n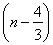
【解析】设Pn＋1(n＋1，an＋1)，则PnPn＋1＝(1，an＋1－an)＝(1,2)，即an＋1－an＝2，所以数列{an}是以2为公差的等差数列．又因为a1＋2a2＝3，所以a1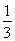＝－，所以Sn＝n.
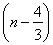