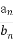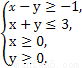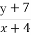题目内容
已知等差数列{an}中,a2+a4=10,a5=9,数列{bn}中,b1=a1,bn+1=bn+an.
(1)求数列{an}的通项公式,写出它的前n项和Sn.
(2)求数列{bn}的通项公式.
(3)若cn=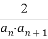 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
(1) an=2n-1,Sn= n2 (2) bn=n2-2n+2 (3) Tn= =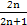
【解析】(1)设{an}的公差为d,由题意得a1=1,d=2,
所以an=2n-1,Sn=na1+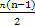 d=n2.
d=n2.
(2)b1=a1=1,bn+1=bn+an=bn+2n-1,
所以b2=b1+1,b3=b2+3=b1+1+3,
bn=b1+1+3+…+(2n-3)=1+(n-1)2=n2-2n+2(n≥2).
又n=1时n2-2n+2=1=b1,
所以数列{bn}的通项公式为bn=n2-2n+2.
(3)cn=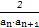 =
=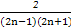 =
=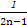 -
-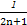 ,
,
Tn=c1+c2+…+cn=(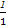 -
-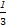 )+(
)+(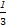 -
-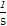 )+…+(
)+…+(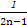 -
-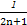 )=1-
)=1-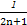 =
=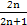 .
.

练习册系列答案
相关题目