题目内容
若二面角α-l-β的大小为
，直线m⊥α，则β所在平面内的直线与m所成角的取值范围是（ ）
| π |
| 3 |
A、(0，
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
分析：根据二面角的平面角大小可知m与β所成的角的大小，考虑特殊位置可得β所在平面内的直线与m所成角，从而求出所求．
解答：解：由二面角α-l-β的大小为
，直线m⊥α，得m与β所成的角的大小为
，
于是β所在平面内的直线与m所成的角的最小值为
，而最大值为
．
故选：C
| π |
| 3 |
| π |
| 6 |
于是β所在平面内的直线与m所成的角的最小值为
| π |
| 6 |
| π |
| 2 |
故选：C
点评：本题主要考查了二面角的应用，以及直线与平面所成角的求解，同时考查了空间想象能力，属于基础题．
练习册系列答案
相关题目
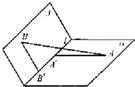如图，α和β为平面，α∩β=l，A∈α，B∈β，AB=5，A，B在棱l上的射影分别为A′，B′，AA′=3，BB′=2．若二面角α-l-β的大小为