题目内容
若二面角α-l-β为
,直线m⊥α,则β所在平面内的直线与m所成角的取值范围是( )
| 2π |
| 3 |
分析:欲求β所在平面内的直线与m所成角的取值范围,即求直线m与β面所成的角,因为β所在平面内的直线与m所成的角中最小的角是线面角,最大的角是
.由此能求出β所在平面内的直线与m所成角的取值范围.
| π |
| 2 |
解答: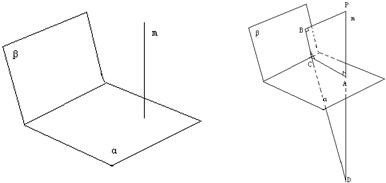 解:欲求β所在平面内的直线与m所成角的取值范围,
解:欲求β所在平面内的直线与m所成角的取值范围,
即求直线m与β面所成的角,
因为β所在平面内的直线与m所成的角中最小的角是线面角,
最大的角是
.
在直线m上取一点P,
过P作PB⊥β,由PA、PB确定的平面交l于C,
则l⊥BC,l⊥CA,
所以∠BCA=
,
BC为直线m在平面β内的射影,
故BC与PA的夹角即为直线m与β面所成的角,
延长BC,PA交于点D,
∵∠BCA=
,PA⊥AC,
∴∠PDB=
,
所以β所在平面内的直线与m所成角的取值范围是:[
,
].
故选D.
 解:欲求β所在平面内的直线与m所成角的取值范围,
解:欲求β所在平面内的直线与m所成角的取值范围,即求直线m与β面所成的角,
因为β所在平面内的直线与m所成的角中最小的角是线面角,
最大的角是
| π |
| 2 |
在直线m上取一点P,
过P作PB⊥β,由PA、PB确定的平面交l于C,
则l⊥BC,l⊥CA,
所以∠BCA=
| 2π |
| 3 |
BC为直线m在平面β内的射影,
故BC与PA的夹角即为直线m与β面所成的角,
延长BC,PA交于点D,
∵∠BCA=
| 2π |
| 3 |
∴∠PDB=
| π |
| 6 |
所以β所在平面内的直线与m所成角的取值范围是:[
| π |
| 6 |
| π |
| 2 |
故选D.
点评:本题考查与二面角有关的立体几何综合题,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
若二面角α-l-β的大小为
,直线m⊥α,则β所在平面内的直线与m所成角的取值范围是( )
| π |
| 3 |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
从空间一点
P向二面角α——l——β的两个面α、β分别作垂线PE、PF,垂足分别为E、F,若二面角α——l——β大小为60°,则∠EPF的大小为[
]|
A .60° |
B .120° |
|
C .60°或120° |
D .不确定 |
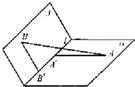 如图,α和β为平面,α∩β=l,A∈α,B∈β,AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角α-l-β的大小为
如图,α和β为平面,α∩β=l,A∈α,B∈β,AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角α-l-β的大小为