题目内容
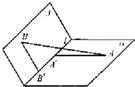 如图,α和β为平面,α∩β=l,A∈α,B∈β,AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角α-l-β的大小为
如图,α和β为平面,α∩β=l,A∈α,B∈β,AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角α-l-β的大小为| 2π | 3 |
(Ⅰ)点B到平面α的距离;
(Ⅱ)异面直线l与AB所成的角(用反三角函数表示).
分析:(1)先过点B到作平面α的垂线,交点为D,∠BB'C为二面角的平面角,再在直角三角形BB'D中求解BD即可;
(2)先通过平移将两条异面直线平移到同一个起点A,得到∠BAC或其补角为异面直线所成的角,在三角形BAC中再利用余弦定理求出此角,再用反三角函数表示即可.
(2)先通过平移将两条异面直线平移到同一个起点A,得到∠BAC或其补角为异面直线所成的角,在三角形BAC中再利用余弦定理求出此角,再用反三角函数表示即可.
解答: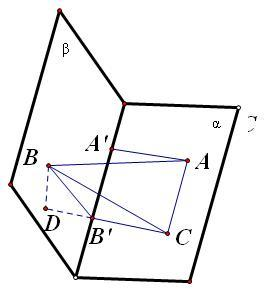 解:(1)如图,过点B′作直线B′C∥A′A且使B′C=A′A.
解:(1)如图,过点B′作直线B′C∥A′A且使B′C=A′A.
过点B作BD⊥CB′,交CB′的延长线于D.
由已知AA′⊥l,可得DB′⊥l,又已知BB′⊥l,
故l⊥平面BB′D,
得BD⊥l又因BD⊥CB′,从而BD⊥平面α,BD之长即为点B到平面α的距离.
因B′C⊥l且BB′⊥l,故∠BB′C为二面角α-l-β的平面角.
由题意,∠BB′C=
.
因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=
,
BD=BB′•sinBB′D=
.
(Ⅱ)连接AC、BC.因B′C∥A′A,B′C=A′A,AA′⊥l,
知A′ACB′为矩形,
故AC∥l.
所以∠BAC或其补角为异面直线l与AB所成的角.
在△BB′C中,B′B=2,B′C=3,∠BB′C=
,
则由余弦定理,
BC=
=
.
因BD⊥平面α,且DC⊥CA,由三垂线定理知AC⊥BC.
故在△ABC中,∠BCA=
,sinBAC=
=
.
因此,异面直线l与AB所成的角为arcsin
 解:(1)如图,过点B′作直线B′C∥A′A且使B′C=A′A.
解:(1)如图,过点B′作直线B′C∥A′A且使B′C=A′A.过点B作BD⊥CB′,交CB′的延长线于D.
由已知AA′⊥l,可得DB′⊥l,又已知BB′⊥l,
故l⊥平面BB′D,
得BD⊥l又因BD⊥CB′,从而BD⊥平面α,BD之长即为点B到平面α的距离.
因B′C⊥l且BB′⊥l,故∠BB′C为二面角α-l-β的平面角.
由题意,∠BB′C=
| 2π |
| 3 |
因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=
| π |
| 3 |
BD=BB′•sinBB′D=
| 3 |
(Ⅱ)连接AC、BC.因B′C∥A′A,B′C=A′A,AA′⊥l,
知A′ACB′为矩形,
故AC∥l.
所以∠BAC或其补角为异面直线l与AB所成的角.
在△BB′C中,B′B=2,B′C=3,∠BB′C=
| 2π |
| 3 |
则由余弦定理,
BC=
| B′B2+B′C2-2B′B•B′C•cos∠BB′C |
| 19 |
因BD⊥平面α,且DC⊥CA,由三垂线定理知AC⊥BC.
故在△ABC中,∠BCA=
| π |
| 2 |
| BC |
| AB |
| ||
| 5 |
因此,异面直线l与AB所成的角为arcsin
| ||
| 5 |
点评:本题主要考查立体几何中的主干知识,如线线角、二面角等基础知识,考查空间想象能力、逻辑思维能力和运算能力.解题的关键是线面平行、三垂线定理等基础知识,本题属中等题.

练习册系列答案
相关题目



 、
、 为平面上的两个定点
为平面上的两个定点 ,
, ,且
,且 ,
, (
( 为动点,
为动点, 是
是 和
和 的交点).
的交点).
 、
、 ,且线段
,且线段 的中垂线与直线
的中垂线与直线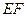 相交于一点
相交于一点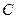 ,证明
,证明 <
< (
( 为
为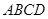 和正
和正
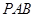 所在平面互相垂直,其中
所在平面互相垂直,其中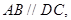
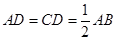 ,且
,且 为
为 中点.
中点. 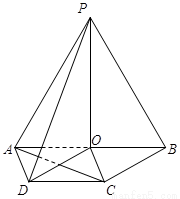
 平面
平面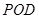 ;
;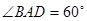 ,求二面角
,求二面角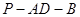 的余弦值;
的余弦值;