题目内容
设数列{an}的首项a1为常数,且an+1=3n-2an(n∈N).
(1)证明:当a1为不等于
的常数时,{an-
}是等比数列;
(2)若a1=
,{an}中是否存在连续三项成等差数列?若存在,说明理由.
(3)若{an}是递增数列,求a1的取值范围.
(1)证明:当a1为不等于
| 3 |
| 5 |
| 3n |
| 5 |
(2)若a1=
| 3 |
| 2 |
(3)若{an}是递增数列,求a1的取值范围.
考点:数列的函数特性,等比关系的确定
专题:等差数列与等比数列
分析:本题(1)根据等比数列的定义,利用条件得到连结两项的比为定值,得到本题结论;(2)假设存符合条件的连续三项,利用等差中项的特征,得到相应关系式,化简得到项数m的值,得到本题结论;(3)对(a1-
)的符号进行分类讨论,得到关于n的恒成立问题,再联系到n的奇偶数情况,求出相关代数式的最值,得到本题结论.
| 3 |
| 5 |
解答:
解:(1)∵an+1=3n-2an(n∈N),
∴an+1-
=3n-2an-
=
×3n-2an=-2(an-
).
∵a1为不等于
的常数时
∴an-
≠0.
∴
=-2.
∴{an-
}是等比数列;
(2){an}中是存在连续三项a2,a3,a4成等差数列,以下证明.
∵a1=
,
∴a1-
=
,
∴{an-
}是以
为首项,以-2为公比的等比数列;
∴an-
=
×(-2)n-1,n∈N*.
∴an=
×(-2)n-1+
,n∈N*.
假设数列{an}中存在连续三项成等差数列,这三项分别为:am,am+1,am+2,
则有:2am+1=am+am+2,
即2×
×(-2)m+2×
=
×(-2)m-1+
+
×(-2)m+1+
,
化简得:(-
)m-1=-
,
∴m=4.
∴{an}中是存在连续三项a4,a5,a6成等差数列.
(3)由(1)知:
(i)当a1=
时,
an=
,an+1=
>
=an,{an}是递增数列;
当a1≠
时,{an-
}是首项为a1-
,公比为-2的等比数列.
∴an-
=(a1-
)×(-2)n-1,
∴an=
+(a1-
)×(-2)n-1,
∵{an}是递增数列,
∴an<an+1,n∈N*.
∴
+(a1-
)×(-2)n-1<
+(a1-
)×(-2)n对于n∈N*恒成立.
∴3(a1-
)(-2)n-1<
×3n,…(*).
(ii)当a1>
时,
①n为偶数时,(-2)n-1<0,(*)式恒成立,
②n为正奇数时,(-2)n-1>0,(*)式可化为:
(a 1-
)<(
)n.
∵(
)n单调递增,∴(
)n≥
,
∴
(a 1-
)<
,
即a1<1.
∴
<a1<1;
(iii)当a1<
时,
①n为正奇数时,(-2)n-1>0,(*)式恒成立,
②n为偶数时,(-2)n-1<0,(*)式可化为:
(a 1-
)>-(
)n,
∵-(
)n单调递减,∴-(
)n≤-(
)2,
∴
(a 1-
)>-
,即a1>0,
∴0<a1<
.
综上,0<a1<1.
∴an+1-
| 3n+1 |
| 5 |
| 3n+1 |
| 5 |
| 2 |
| 5 |
| 3n |
| 5 |
∵a1为不等于
| 3 |
| 5 |
∴an-
| 3n |
| 5 |
∴
an+1-
| ||
an-
|
∴{an-
| 3n |
| 5 |
(2){an}中是存在连续三项a2,a3,a4成等差数列,以下证明.
∵a1=
| 3 |
| 2 |
∴a1-
| 3 |
| 5 |
| 9 |
| 10 |
∴{an-
| 3n |
| 5 |
| 9 |
| 10 |
∴an-
| 3n |
| 5 |
| 9 |
| 10 |
∴an=
| 9 |
| 10 |
| 3n |
| 5 |
假设数列{an}中存在连续三项成等差数列,这三项分别为:am,am+1,am+2,
则有:2am+1=am+am+2,
即2×
| 9 |
| 10 |
| 3m+1 |
| 5 |
| 9 |
| 10 |
| 3m |
| 5 |
| 9 |
| 10 |
| 3m+2 |
| 5 |
化简得:(-
| 3 |
| 2 |
| 27 |
| 8 |
∴m=4.
∴{an}中是存在连续三项a4,a5,a6成等差数列.
(3)由(1)知:
(i)当a1=
| 3 |
| 5 |
an=
| 3n |
| 5 |
| 3n+1 |
| 5 |
| 3n |
| 5 |
当a1≠
| 3 |
| 5 |
| 3n |
| 5 |
| 3 |
| 5 |
∴an-
| 3n |
| 5 |
| 3 |
| 5 |
∴an=
| 3n |
| 5 |
| 3 |
| 5 |
∵{an}是递增数列,
∴an<an+1,n∈N*.
∴
| 3n |
| 5 |
| 3 |
| 5 |
| 3n+1 |
| 5 |
| 3 |
| 5 |
∴3(a1-
| 3 |
| 5 |
| 2 |
| 5 |
(ii)当a1>
| 3 |
| 5 |
①n为偶数时,(-2)n-1<0,(*)式恒成立,
②n为正奇数时,(-2)n-1>0,(*)式可化为:
| 15 |
| 4 |
| 3 |
| 5 |
| 3 |
| 2 |
∵(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴
| 15 |
| 4 |
| 3 |
| 5 |
| 3 |
| 2 |
即a1<1.
∴
| 3 |
| 5 |
(iii)当a1<
| 3 |
| 5 |
①n为正奇数时,(-2)n-1>0,(*)式恒成立,
②n为偶数时,(-2)n-1<0,(*)式可化为:
| 15 |
| 4 |
| 3 |
| 5 |
| 3 |
| 2 |
∵-(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴
| 15 |
| 4 |
| 3 |
| 5 |
| 9 |
| 4 |
∴0<a1<
| 3 |
| 5 |
综上,0<a1<1.
点评:本题考查了等差数列、等比数列的定义,还重点考查了分类讨论、化归转化的数学思想,本题有一定的难度和计算量,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
若tanx=2则cos2x=( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
设全集U={x∈N*|x<6},集合A={1,3},∁UB={3,5},则A∩B=( )
| A、{1} | B、{1,5} |
| C、{4} | D、{2} |
已知a=log
3,b=log
2,c=20.3,则a,b,c三者的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、c>b>a |
| B、a>c>b |
| C、b>a>c |
| D、c>a>b |
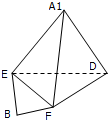 如图,边长为2的正方形ABCD中,E是AB边上的点,F是边BC上的点,且BE=BF,若将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1.
如图,边长为2的正方形ABCD中,E是AB边上的点,F是边BC上的点,且BE=BF,若将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1.