题目内容
【题目】函数![]()
(1)若![]() 是定义域上的单调函数,求
是定义域上的单调函数,求![]() 的取值范围.
的取值范围.
(2)设![]() ,
,![]() 分别为
分别为![]() 的极大值和极小值,若
的极大值和极小值,若![]() ,求
,求![]() 取值范围.
取值范围.
【答案】(1) ![]() 或
或![]() (2)
(2) ![]()
【解析】
(1)首先求函数![]() 的定义域以及导函数
的定义域以及导函数![]() ,由
,由![]() 是定义域上的单调函数等价于导函数在定义域范围内恒大于等于零或恒小于等于零,分别令导函数大于等于零或恒小于等于零,分离参数
是定义域上的单调函数等价于导函数在定义域范围内恒大于等于零或恒小于等于零,分别令导函数大于等于零或恒小于等于零,分离参数![]() ,即可求出
,即可求出![]() 的取值范围;
的取值范围;
(2)设![]() 的两根为
的两根为![]() ,可得
,可得![]() ,
,![]() ,将
,将![]() ,代入化简,构造函数
,代入化简,构造函数![]() ,求导数,应用单调性,即可得到
,求导数,应用单调性,即可得到![]() 的范围.
的范围.
(1) 函数![]() 是定义域为
是定义域为![]() ,
,![]() ,
,
由![]() 是定义域上的单调函数等价于导函数在定义域范围内恒大于等于零或恒小于等于零
是定义域上的单调函数等价于导函数在定义域范围内恒大于等于零或恒小于等于零
①令![]() ,即
,即![]() ,则
,则![]() 恒成立,∴
恒成立,∴![]()
②令![]() ,即
,即![]() ,则
,则![]() 恒成立,∴
恒成立,∴![]()
综上,![]() 或
或![]()
(2)由![]() 且
且![]() 得
得![]()
此时设![]() 的两根为
的两根为![]() ,
,
所以![]()
因为![]() ,
,
所以![]() ,
,
由![]() ,且
,且![]() 得
得![]()
所以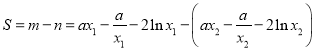
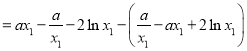
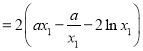
由![]() 得
得![]() 代入上式得
代入上式得
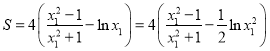
令![]() ,
,
所以![]() ,
,
![]() ,
,
则![]() ,
,
![]()
所以![]() 在
在![]() 上为减函数
上为减函数
从而![]() ,即
,即![]()
所以![]() .
.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
【题目】某研究性学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如表经计算![]() ,则下列选项正确的是( )
,则下列选项正确的是( )
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
附表
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
A. 有99.5%的把握认为使用智能手机对学习有影响
B. 有99.5%的把握认为使用智能手机对学习无影响
C. 有99.9%的把握认为使用智能手机对学习有影响
D. 有99.9%的把握认为使用智能手机对学习无影响

