题目内容
【题目】已知![]() ,
,![]() 是实常数.
是实常数.
(1)当![]() 时,判断函数
时,判断函数![]() 的奇偶性,并给出证明;
的奇偶性,并给出证明;
(2)若![]() 是奇函数,不等式
是奇函数,不等式![]() 有解,求
有解,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 为非奇非偶函数,证明见解析;(2)
为非奇非偶函数,证明见解析;(2)![]() .
.
【解析】
(1)当![]() 时,
时,![]() ,计算
,计算![]() 不相等,也不互为相反数,可得出结论;
不相等,也不互为相反数,可得出结论;
(2)由奇函数的定义,求出![]() 的值,证明
的值,证明![]() 在
在![]() 上单调递减,
上单调递减,![]() 有解,化为
有解,化为![]() 有解,求出
有解,求出![]() 的值域,即可求解.
的值域,即可求解.
(1)![]() 为非奇非偶函数.
为非奇非偶函数.
当![]() 时,
时,![]() ,
,![]() ,
,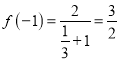 ,
,
因为![]() ,所以
,所以![]() 不是偶函数;
不是偶函数;
又因为![]() ,所以
,所以![]() 不是奇函数,
不是奇函数,
即![]() 为非奇非偶函数.
为非奇非偶函数.
(2)因为![]() 是奇函数,所以
是奇函数,所以![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
化简整理得![]() ,即
,即![]() .
.
下用定义法研究![]() 的单调性;
的单调性;
设任意![]() ,且
,且
![]() ,
,![]()
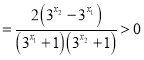 ,
,
所以函数![]() 在
在![]() 上单调递减,
上单调递减,
因为![]() 有解,且函数为奇函数,
有解,且函数为奇函数,
所以![]() 有解,
有解,
又因为函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以
![]() 有解,
有解,![]()
![]() ,
,![]() 的值域为
的值域为![]() ,
,
所以![]() ,即
,即![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】美国一贯推行强权政治,2018年3月22日,美国总统特朗普在白宫签署了对中国输美产品征收关税的总统备忘录,限制中国商品进入美国市场。中国某企业计划打入美国市场,决定从A、B两种产品中只选一种进行投资生产,已知投入生产这两种产品的有关数据如下表:(单位:万元)
年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产件数 | |
A产品 | 40 | m | 15 | 200 |
B产品 | 60 | 10 | 22 | 150 |
其中固定成本与年生产的件数无关,m是待定的常数,其值由生产A产品的原材料决定,预计![]() ,另外,年销售
,另外,年销售![]() 件B产品时需交0.05
件B产品时需交0.05![]() 万元的附件关税,假设生产出来的产品都能在当年销售出去.
万元的附件关税,假设生产出来的产品都能在当年销售出去.
(1)求该厂分别投资生产A、B两种产品的年利润![]() 与生产相应产品的件数
与生产相应产品的件数![]() 之间的函数关系,并求出其定义域;
之间的函数关系,并求出其定义域;
(2)如何投资才可获得最大年利润?请设计出投资方案.



