Question

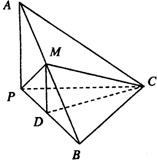21、如图，在三棱锥A-BPC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且△PMB为正三角形，
（Ⅰ）求证：MD∥平面APC；
（Ⅱ）求证：平面ABC⊥平面APC．

Answer 1

分析：（Ⅰ）∵M为AB中点，D为PB中点，由中位线定理得MD∥AP，由线面平行的判定证得MD∥平面APC；
（Ⅱ）先证得AP⊥BC，又有AC⊥BC，通过线面垂直的判定证出BC⊥平面APC，再由面面垂直的判定证出平面ABC⊥平面PAC．

解答：证明：（Ⅰ）∵M为AB中点，D为PB中点，
∴MD∥AP，
又MD?平面ABC，
∴MD∥平面APC．
（Ⅱ）∵△PMB为正三角形，且D为PB中点，
∴MD⊥PB．
又由（Ⅰ）知MD∥AP，
∴AP⊥PB．
又已知AP⊥PC，PB∩PC=P
∴AP⊥平面PBC，而BC包含于平面PBC，
∴AP⊥BC，
又AC⊥BC，而AP∩AC=A，
∴BC⊥平面APC，
又BC包含于平面ABC
∴平面ABC⊥平面PAC．

点评：本题主要是通过线线、线面、面面之间的关系的转化来考查线线、线面、面面的判定定理．