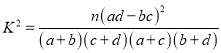题目内容
【题目】某种产品每件成本为6元,每件售价为![]() 元(
元(![]() ),年销售
),年销售![]() 万件,若已知
万件,若已知![]() 与
与![]() 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(1)求年销售利润![]() 关于售价
关于售价![]() 的函数关系式.
的函数关系式.
(2)求售价为多少时,年利润最大,并求出最大年利润.
【答案】(I)![]() (II) 售价为9元时,年利润最大,最大年利润为135万元
(II) 售价为9元时,年利润最大,最大年利润为135万元
【解析】试题分析:(1)根据题中条件:“若已知![]() 与
与![]() 成正比,可设
成正比,可设![]() 再依据售价为10元时,年销量为28万件求得k值,从而得出年销售利润y关于x的函数关系式.
再依据售价为10元时,年销量为28万件求得k值,从而得出年销售利润y关于x的函数关系式.
(2)利用导数研究函数的最值,先求出y的导数,根据y′>0求得的区间是单调增区间,y′<0求得的区间是单调减区间,从而求出极值进而得出最值即可.
试题解析:
(I)设![]()
![]() 售价为10元时, 年销量为28万件,
售价为10元时, 年销量为28万件,
![]()
![]() ,解得
,解得![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
(II)![]()
![]()
令![]() ,得
,得![]() (舍去),或
(舍去),或![]()
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
![]() 函数
函数![]() 在
在![]() 上是递增的, 在
上是递增的, 在![]() 上是递减的.
上是递减的.
![]() 当
当![]() 时,
时,![]() 取最大值,且
取最大值,且![]()
![]() 售价为9元时,年利润最大,最大年利润为135万元.
售价为9元时,年利润最大,最大年利润为135万元.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
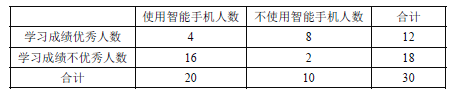
【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:( )
做不到“光盘” | 能做到“光盘” | |
男 | 45 | 10 |
女 | 30 | 15 |
附:
P(K2 | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
![]()
参照附表,得到的正确结论是
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”