Question

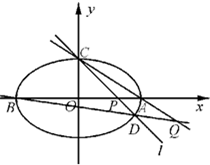过点C（0，1）的椭圆

x2

a2

+

y2

b2

=1 (a＞b＞0)的离心率为

3

2

，椭圆与x轴交于两点A（a，0）、B（-a，0），过点C的直线l与椭圆交于另一点D，并与x轴交于点P，直线AC与直线BD交于点Q．
（1）求椭圆的方程；
（2）当直线l过椭圆右焦点时，求线段CD的长；
（3）当点P异于点B时，求证：

OP

•

OQ

为定值．

Answer 1

分析：（1）由已知得b=1，

c

a

=

3

2

，由a²=c²+b²可求a，b，进而可求椭圆方程
（2）由椭圆的右焦点为(

3

，0)，可得直线l的方程为 y=-

3

3

x+1，联立椭圆方程可求D，根据弦长公式可求CD
（3）当直线l与x轴垂直时与题意不符，故设直线l的方程为y=kx+1(k≠0且k≠

1

2

)．代入椭圆方程可求D点的坐标，联立直线AC，直线BD的方程可求Q，结合已知P可求

OP

，

OQ

，根据向量的数量积的坐标表示代入可证

解答：解：（1）由已知得b=1，

c

a

=

3

2

，由a²=c²+b²=c²+1
解得a=2，
故椭圆方程为

x2

4

+y2=1．…（3分）
（2）椭圆的右焦点为(

3

，0)，此时直线l的方程为 y=-

3

3

x+1，
代入椭圆方整理可得，7x2-8

3

x=0，解得x1=0，x2=

8 3

7

，
代入直线l的方程得 y1=1，y2=-

1

7

，所以D(

8 3

7

，-

1

7

)，
故|CD|=

( 8 3 7 -0)2+(- 1 7 -1)2

=

16

7

．…（6分）
（3）当直线l与x轴垂直时与题意不符．…（7分）
设直线l的方程为y=kx+1(k≠0且k≠

1

2

)．代入椭圆方程得（4k²+1）x²+8kx=0．
解得x1=0，x2=

-8k

4k2+1

，代入直线l的方程得y1=1，y2=

1-4k2

4k2+1

，
所以D点的坐标为(

-8k

4k2+1

，

1-4k2

4k2+1

)．…（10分）
又直线AC的方程为

x

2

+y=1，又直线BD的方程为y=

1+2k

2-4k

(x+2)，联立得

x=-4k y=2k+1.

因此Q（-4k，2k+1），又P(-

1

k

，0)．
所以

OP

•

OQ

=(-

1

k

，0)(-4k，2k+1)=4．
故

OP

•

OQ

为定值．…（14分）

点评：本题主要考察了由椭圆的性质求解椭圆方程，直线与曲线相交的弦长公式的应用及向量的数量积的坐标表示的应用，属于圆锥曲线问题的综合应用