题目内容

椭圆C的方程
x2
a2
+
y2
b2
=1(a＞b＞0)，斜率为1的直L与椭C交于A（x1，y1）B（x2，y2）两点．
（Ⅰ）若椭圆的离心率e=
3
2
，直线l过点M（b，0），且
OA
•
OB
=-
12
5
，求椭圆C的方程；
（Ⅱ）直线l过椭圆的右焦点F，设向量
OP
=λ（
OA
+
OB
）（λ＞0），若点P在椭C上，λ的取值范围．
分析：（Ⅰ）由e=
3
2
，知a=2b，c=
3
b．由
y=x-b
x2+4y2=4b2
，知A(
8b
5
，
3b
5
)，B（0，-b）．再由
OA
•
OB
=-
12
5
能推导出椭圆C的方程．
（Ⅱ）由
y=x-c
b2x2+a2y2=a2b2
，得（b2+a2）x2-2a2cx+a2（c2-b2）=0，由韦达定理知
OA
+
OB
=(
2a2c
a2+b2
，
-2b2c
a2+b2
)，
OP
=(
2λa2c
a2+b2
，
-2λb2c
a2+b2
 )．再由点P在椭圆C上，知λ2=
a2+b2
4c2
=
2a2-c2
4c2
=
1
2e2
-
1
4
＞
1
4
，由此能导出λ的取值范围．
解答：解：（Ⅰ）∵e=
3
2
，∴a=2b，c=
3
b．
y=x-b
x2+4y2=4b2
，
∴A(
8b
5
，
3b
5
)，B（0，-b）．
∵
OA
•
OB
=-
12
5
，∴-
3b2
5
=-
12
5
，b2=4，a2=16．
∴椭圆C的方程为
x2
16
+
y2
4
=1．（5分）
（Ⅱ）由
y=x-c
b2x2+a2y2=a2b2
，
得（b2+a2）x2-2a2cx+a2（c2-b2）=0，
x1+x2 =
2a2c
a2+b2
，y1+y2=
-2b2c
a2+b2
．
OA
+
OB
=(
2a2c
a2+b2
，
-2b2c
a2+b2
)，
OP
=(
2λa2c
a2+b2
，
-2λb2c
a2+b2
 )．
∵点P在椭圆C上，将点P坐标代入椭圆方程中得λ2=
a2+b2
4c2
．
∵b2+c2=a2，0＜e＜1，
∴λ2=
a2+b2
4c2
=
2a2-c2
4c2
=
1
2e2
-
1
4
＞
1
4
，
∴λ＞
1
2
．（12分）
点评：本题考查椭圆方程的求法和求实数λ的取值范围．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
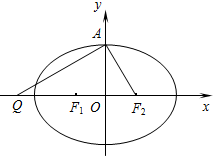精英家教网设椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2，上顶点为A，过点A与AF2垂直的直线交x轴负半轴于点Q，且2
F1F2
+
F2Q
=0，若过A，Q，F2三点的圆恰好与直线l：x-
3
y-3=0相切．过定点M（0，2）的直线l1与椭圆C交于G，H两点（点G在点M，H之间）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设直线l1的斜率k＞0，在x轴上是否存在点P（m，0），使得以PG，PH为邻边的平行四边形是菱形．如果存在，求出m的取值范围，如果不存在，请说明理由；
（Ⅲ）若实数λ满足
MG
=λ
MH
，求λ的取值范围．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
1
2
，且经过点P(1，
3
2
)．
（1）求椭圆C的方程；
（2）设F是椭圆C的左焦，判断以PF为直径的圆与以椭圆长轴为直径的圆的位置关系，并说明理由．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，F(
2
，0)为其右焦点，过F垂直于x轴的直线与椭圆相交所得的弦长为2．
（1）求椭圆C的方程；
（2）直线l：y=kx+m（km≠0）与椭圆C交于A、B两点，若线段AB中点在直线x+2y=0上，求△FAB的面积的最大值．
（2013•肇庆二模）设F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左右焦点．
（1）设椭圆C上的点(
2
2
，
3
2
)到F1，F2两点距离之和等于2
2
，写出椭圆C的方程；
（2）设过（1）中所得椭圆上的焦点F2且斜率为1的直线与其相交于A，B，求△ABF1的面积；
（3）设点P是椭圆C 上的任意一点，过原点的直线l与椭圆相交于M，N两点，当直线PM，PN的斜率都存在，并记为kPN，kPN试探究kPN•kPN的值是否与点P及直线l有关，并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网