题目内容
给出下列命题:
①已知a,b,m都是正数,且
>
,则a<b;
②已知f'(x)是f(x)的导函数,若?x∈R,f'(x)≥0,则f(1)<f(2)一定成立;
③命题“?x∈R,使得x2-2x+1<0”的否定是真命题;
④“x≤1,且y≤1”是“x+y≤2”的充要条件.
其中正确命题的序号是
①已知a,b,m都是正数,且
| a+1 |
| b+1 |
| a |
| b |
②已知f'(x)是f(x)的导函数,若?x∈R,f'(x)≥0,则f(1)<f(2)一定成立;
③命题“?x∈R,使得x2-2x+1<0”的否定是真命题;
④“x≤1,且y≤1”是“x+y≤2”的充要条件.
其中正确命题的序号是
①③
①③
.(把你认为正确命题的序号都填上)分析:对于:①②③④中的②④可通过举反例进行否定:对于②若f(x)是常数函数,则f(1)<f(2)不成立;故错;
对于④若“x=1.8,且y=0.1”则“x+y≤2”不能推得“x≤1,且y≤1”故④错;对于①③可根据不等式的性质进行证明其正确性.
对于④若“x=1.8,且y=0.1”则“x+y≤2”不能推得“x≤1,且y≤1”故④错;对于①③可根据不等式的性质进行证明其正确性.
解答:解:对于:
①已知a,b,m都是正数,且
>
⇒ab+b>ab+a⇒a<b;正确;
②若f(x)是常数函数,则f(1)<f(2)不成立;故错;
③命题“?x∈R,使得x2-2x+1<0”的否定是“?x∈R,使得x2-2x+1≥0”真命题;正确;
④若“x=1.8,且y=0.1”则“x+y≤2”不能推得“x≤1,且y≤1”故④错;
正确命题的序号是①③.
故答案为:①③.
①已知a,b,m都是正数,且
| a+1 |
| b+1 |
| a |
| b |
②若f(x)是常数函数,则f(1)<f(2)不成立;故错;
③命题“?x∈R,使得x2-2x+1<0”的否定是“?x∈R,使得x2-2x+1≥0”真命题;正确;
④若“x=1.8,且y=0.1”则“x+y≤2”不能推得“x≤1,且y≤1”故④错;
正确命题的序号是①③.
故答案为:①③.
点评:本小题主要考查命题的否定、不等关系与不等式等基础知识,通过举反例可证明一个命题为假.属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.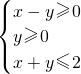 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.