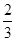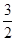题目内容
已知等比数列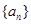 为正项递增数列,且
为正项递增数列,且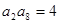 ,
,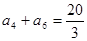 ,数列
,数列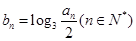 .
.
(1)求数列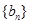 的通项公式;
的通项公式;
(2)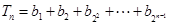 ,求
,求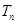 .
.
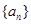 为正项递增数列,且
为正项递增数列,且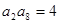 ,
,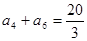 ,数列
,数列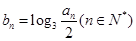 .
.(1)求数列
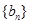 的通项公式;
的通项公式;(2)
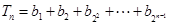 ,求
,求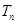 .
.(1)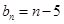 ;(2)
;(2) .
.
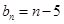 ;(2)
;(2) .
.试题分析:(1)首先要求出数列
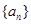 的通项
的通项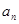 ,根据题设条件可采取基本量法,也可应用等比数列的性质,如
,根据题设条件可采取基本量法,也可应用等比数列的性质,如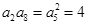 ,
,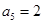 ,
,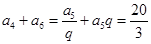 ,可解得
,可解得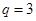 或
或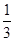 ,数列
,数列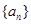 又是递增的数列,这样取
又是递增的数列,这样取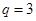 ,由此可得
,由此可得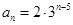 ,于是有
,于是有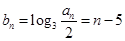 ;(2)要求
;(2)要求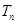 ,我们应该确定它是哪个数列的前
,我们应该确定它是哪个数列的前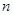 项和,从已知可能看出,可设
项和,从已知可能看出,可设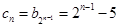 ,因此求
,因此求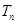 时可用分组求和的方法,化为一个等比数列的和与一个常数列的和,即
时可用分组求和的方法,化为一个等比数列的和与一个常数列的和,即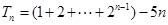 .
.试题解析:(1)∵{an}是正项等比数列,

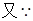
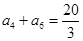
两式相除得:
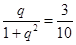 . 2分
. 2分∴q=3或者q=
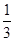 ,
,∵{an}为增数列,∴q=3,a1=
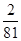 . 4分
. 4分∴an=a1qn-1=
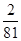 ·3n-1=2·3n-5.∴bn=log3
·3n-1=2·3n-5.∴bn=log3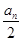 =n-5. 6分
=n-5. 6分(2)Tn=
 =(1-5)+(2-5)+(22-5)+ +(2n-1-5)
=(1-5)+(2-5)+(22-5)+ +(2n-1-5)=
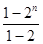 -5n=
-5n=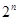 -5n-1 12分(三步,每步2分)
-5n-1 12分(三步,每步2分)
练习册系列答案
相关题目
 的首项
的首项 .
. 为等比数列;
为等比数列; ,若
,若 ,求最大正整数
,求最大正整数 的值;
的值; ,使
,使 成等比数列?如果存在,请给予证明;如果不存在,请说明理由.
成等比数列?如果存在,请给予证明;如果不存在,请说明理由. ,若
,若 +
+ =20,
=20, +
+ =80,则
=80,则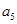 +
+ 等于( )
等于( ) 中,
中, =1,
=1, (
( ,则
,则 为
为



 中,
中,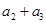 =1,
=1,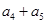 =2,则
=2,则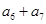 等于( ).
等于( ).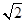
 的公比为
的公比为 ,前
,前 项和为
项和为 ,且
,且 .若
.若 ,则
,则



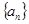 是无穷等比数列,其前n项和是
是无穷等比数列,其前n项和是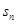 ,若
,若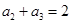 ,
,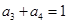 ,则
,则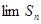 的值为.( )
的值为.( )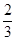
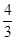
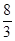
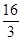
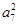 =4π,则tan(a2a12)的值为( )
=4π,则tan(a2a12)的值为( )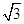
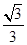
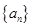 中,
中,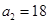 ,
,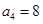 ,则数列
,则数列