题目内容
【题目】已知函数f(x)=![]() ,g(x)=a
,g(x)=a![]()
(1)当a=3时,解不等式(关于x的)f(x)![]() g(x)+3.
g(x)+3.
(2)若f(x)![]() g(x)-1 对于任意x
g(x)-1 对于任意x![]() 都成立,求a的取值范围。
都成立,求a的取值范围。
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)写出不等式,根据绝对值零点进行分段求解即可,最后各段结果取并集.
(2)对自变量进行分类讨论,分离参数,利用绝对值三角不等式求解即可.
(1)当a=3 时![]() >3
>3![]() +3即
+3即![]() -3
-3![]() -3>0
-3>0
①当X≤0时4-x+3x-3>0即x>-![]() 即-
即-![]() <x<0
<x<0
②当0<x<4时4-x-3x-3>0即x<-![]() (舍去)
(舍去)
③当X≥4时x-4-3X-3>0即X<-![]()
综上所述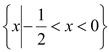
(2)若不等式f(x)≥g(x)-4恒成立即![]() ≥a
≥a![]() -4即a
-4即a![]() ≤
≤![]() +4
+4
当x=0时0≤8成立
当x≠0时a≤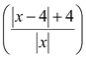
![]() ,因为
,因为![]() +4≥
+4≥![]() =
=![]() >0
>0
所以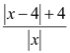 ≥1(当且仅当x=4时取“等号”)
≥1(当且仅当x=4时取“等号”)
所以 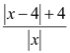 的最小值为1,所以a的取值范围是
的最小值为1,所以a的取值范围是![]()

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
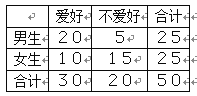
【题目】郑州一中社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图:将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“围棋迷”与性别有关?

非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望
附:![]() ,
,
| 0.05 | 0.01 |
| 3.841 | 6.635 |