题目内容
15．函数f（x）=2|x-1|-x+1的最小值为0．分析 讨论当x≥1时，当x＜1时，去绝对值，运用一次函数的单调性，即可得到所求最小值．
解答 解：当x≥1时，f（x）=2（x-1）-x+1=x-1，即有f（x）≥0；
当x＜1时，f（x）=2（1-x）-x+1=3-3x，
即有f（x）＞0．
则当x=1时，f（x）取得最小值，且为0．
故答案为：0．
点评 本题考查绝对值函数的最值的求法，注意由绝对值的含义去绝对值，运用一次函数的单调性，属于基础题．
练习册系列答案
相关题目
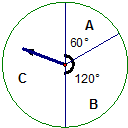五一节期间，某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券．（假定指针等可能地停在任一位置，指针落在区域的边界时，重新转一次）指针所在的区域及对应的返劵金额见右上表．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．