题目内容
设等比数列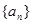 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
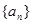 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为  2
2 试题分析:设等比数列{an}的公比为q,前n项和为Sn,且Sn+1,Sn,Sn+2成等差数列,则2Sn=Sn+1+Sn+2 .
若q=1,则Sn=na1,式显然不成立.
若q≠1,则
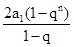 =
=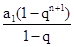 +
+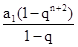
故2qn=qn+1+qn+2,即q2+q-2=0,因此q=-2.
点评:涉及等比数列求和时,若公比为字母,则需要分类讨论,属中档题.

练习册系列答案
相关题目
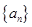 的各项均为正数,且
的各项均为正数,且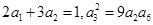
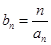 ,求数列
,求数列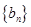 的前n项和
的前n项和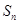 .
.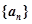 中,
中,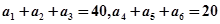 ,则前9项之和等于( )
,则前9项之和等于( )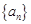 为公比
为公比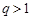 的等比数列,若
的等比数列,若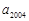 和
和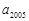 是方程
是方程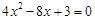 的两根,则
的两根,则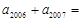 ______.
______.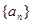 的首项
的首项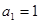 ,公比为
,公比为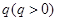 ,前
,前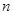 项和为
项和为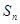 ,若
,若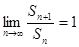 ,则公比
,则公比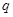 的取值范围是 .
的取值范围是 .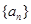 的前
的前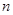 项和为
项和为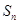 ,若
,若 ,则
,则 .
.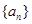 中,
中,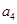 与
与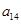 的等比中项为
的等比中项为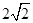 ,则
,则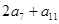 的最小值为 .
的最小值为 .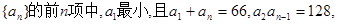 前n项和
前n项和 求
求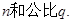
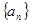 的各项均为正数,若
的各项均为正数,若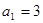 ,前三项的和为21 ,则
,前三项的和为21 ,则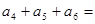 。
。