题目内容
7．不等式2x-$\sqrt{x}$＜1的解集为[0，1）．分析 令t=$\sqrt{x}$，t≥0，则x=t2，则不等式2x-$\sqrt{x}$＜1可化为：2t2-t＜1，先求t的范围，进而可得原不等式的解集．
解答 解：令t=$\sqrt{x}$，t≥0，则x=t2，
则不等式2x-$\sqrt{x}$＜1可化为：2t2-t＜1，
解得：t∈（$-\frac{1}{2}$，1），
即t∈[0，1），
∴x∈[0，1），
即原不等式的解集为：[0，1），
故答案为：[0，1）
点评 本题考查的是根式不等式的解法，分类讨论思想，难度中档．
练习册系列答案
快乐5加2金卷系列答案
相关题目
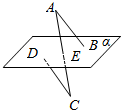如图，已知AB∥CD，AB∩α=B，CD∩α=D，AC∩α=E，求证：E，B，D三点共线．