Question

【题目】已知定义在（1，+∞）上的函数f（x）=．

（1）当m≠0时，判断函数f（x）的单调性，并证明你的结论；

（2）当m=时，求解关于x的不等式f（x2-1）＞f（3x-3）．

Answer 1

【答案】（1）见解析；（2）（，2）

【解析】

(1)利用函数单调性的定义进行证明即可;(2)利用函数的单调性写出满足的不等式组,从而可得不等式的解集.

（1）根据题意，设1＜x1＜x2，

则f（x1）-f（x2）=-=m×，

又由1＜x1＜x2，则（x2-x1）＞0，（x2-1）＞0，（x1-1）＞0，

当m＞0时，f（x1）＞f（x2），f（x）在（1，+∞）上递减；

当m＜0时，f（x1）＜f（x2），f（x）在（1，+∞）上递增；

（2）当m=时，f（x）为减函数，则f（x2-1）＞f（3x-3），

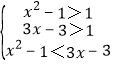解可得：＜x＜2，

即不等式的解集为（，2）