Question

【题目】如图为一个缆车示意图，该缆车半径为4.8m，圆上最低点与地面距离为0.8m,60秒转动一圈，图中OA与地面垂直，以OA为始边，逆时针转动θ角到OB，设B点与地面距离是h.

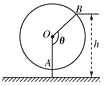
(1)求h与θ间的函数关系式；

(2)设从OA开始转动，经过t秒后到达OB，求h与t之间的函数关系式，并求缆车到达最高点时用的最少时间是多少？

Answer 1

【答案】(1)以圆心O为原点，建立如图所示的平面直角坐标系，

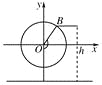
则以Ox为始边，OB为终边的角为θ－，

故点B的坐标为

(4.8cos，4.8sin)，

∴h＝5.6＋4.8sin.

(2)点A在圆上转动的角速度是，故t秒转过的弧度数为t，

∴h＝5.6＋4.8sin，t∈[0，＋∞)．

到达最高点时，h＝10.4 m.

由sin＝1

得t－＝，

∴t＝30

∴缆车到达最高点时，用的时间最少为30秒

【解析】

（1）建立平面直角坐标系，结合条件求出点的坐标后可得h与θ间的函数关系式．（2）由t s转过的弧度数为可得θ与t的关系，代入（1）中的关系式可得h与t之间的函数解析式，然后通过最值可得所求的最小时间．

(1)以圆心原点，建立如图所示的坐标系，如下图所示，

则以为始边，为终边的角为，

故点B坐标为．

∴．

（2）点A在圆上转动的角速度是，故t s转过的弧度数为，

∴，

∴．

令，

得，

∴，

∴．

令，得t=30 s．

∴缆车到达最高点时，用的时间最少为30 s．